Calculo matricial con NumPy

23 de abril del 2021

1. Resumen

Vamos a ver una pequeña introducción a la librería de cálculo matricial NumPy. Esta librería está diseñada para todo tipo de cálculo matricial, por lo que nos vamos a quedar solo con la parte que nos será útil para entender los cálculos dentro de las redes neuronales, pero nos dejaremos fuera cosas interesantes como el uso de la librería para el álgebra lineal

2. ¿Qué es NumPy?

NumPy es una librería de Python diseñada para realizar cálculo matricial. El cálculo matricial es algo que se utiliza mucho en ciencia en general y en data science en particular, por lo que es necesario tener una librería que haga esto muy bien.

Su nombre quiere decir Numerical Python

Su objeto principal es el ndarray, que encapsula matrices de dimensión n de tipos de datos homogéneos, a diferencia de las listas de Python, que pueden tener datos de distintos tipos.

NumPy tiene el objetivo de realizar el cálculo matricial mucho más rápido que con las listas de Python, pero ¿cómo es esto posible?

NumPy utiliza código compilado, mientras que Python utiliza código interpretado. La diferencia es que Python en el momento de ejecución tiene que interpretar, compilar y ejecutar el código, mientras que NumPy ya está compilado, por lo que se ejecuta más rápido
Los ndarrays tienen un tamaño fijo, a diferencia de las listas de Python que son dinámicas. Si en NumPy se quiere modificar el tamaño de una matriz, se creará una nueva y se eliminará la antigua
Todos los elementos de los ndarrays son del mismo tipo de dato, a diferencia de las listas de Python que pueden tener elementos de distintos tipos
Parte del código de NumPy está escrita en C/C++ (mucho más rápida que Python)
Los datos de las matrices se almacenan en memoria de manera continua, a diferencia de las listas de Python, lo que hace que sea mucho más rápido manipularlos

NumPy ofrece la facilidad de usar código sencillo de escribir y de leer, pero que está escrito y precompilado en C, lo que lo hace mucho más rápido.

Supongamos que queremos multiplicar dos vectores, esto se haría en C de la siguiente manera:

for (i = 0; i < rows; i++): {
  for (j = 0; j < columns; j++): {
    c[i][j] = a[i][j]*b[i][j];
  }
}

NumPy ofrece la posibilidad de ejecutar este código por debajo, pero de una manera mucho más fácil de escribir y de entender mediante

c = a * b

NumPy ofrece código vectorizado, que supone no tener que escribir bucles, pero que sin embargo sí están siendo ejecutados por debajo en código C optimizado y precompilado. Esto tiene las siguientes ventajas:

El código es más fácil de escribir y de leer
Al necesitarse menos líneas de código, hay menor probabilidad de introducir errores
El código se parece más a la notación matemática

2.1. NumPy como `np`

Generalmente a la hora de importar NumPy se suele importar con el alias de np

	
		
			< >
			Input
		
		
			Python
			
		
	
	
		import numpy as np
 
print(np.__version__)
	
	Copied

>_ Output

			
				1.18.1

3. Velocidad de NumPy

Como se ha explicado, NumPy realiza el cálculo mucho más rápido que las listas de Python, veamos un ejemplo en el que se realiza el producto escalar de dos matrices, mediante listas de Python y mediante ndarrays

	
		
			< >
			Input
		
		
			Python
			
		
	
	
		from time import time
 
# Dimensión de las matrices
dim = 1000
shape = (dim, dim)
 
# Se crean dos ndarrays de NumPy de dimensión dim x dim
ndarray_a = np.ones(shape=shape)
ndarray_b = np.ones(shape=shape)
 
# Se crean dos listas de Python de dimensión dim x dim a partir de los ndarrays
list_a = list(ndarray_a)
list_b = list(ndarray_b)
 
# Se crean el ndarray y la lista de Python donde se guardarán los resultados
ndarray_c = np.empty(shape=shape)
list_c = list(ndarray_c)
 
# Producto escalar de dos listas de python
t0 = time()
for fila in range(dim):
  for columna in range(dim):
    list_c[fila][columna] = list_a[fila][columna] * list_b[fila][columna]
t = time()
t_listas = t-t0
print(f"Tiempo para realizar el producto escalar de dos listas de Python de dimensiones {dim}x{dim}: {t_listas:.4f} ms")
 
 
# Producto escalar de dos ndarrays de NumPy
t0 = time()
ndarray_c = ndarray_a * ndarray_b
t = time()
t_ndarrays = t-t0
print(f"Tiempo para realizar el producto escalar de dos ndarrays de NumPy de dimensiones {dim}x{dim}: {t_ndarrays:.4f} ms")
 
# Comparación de tiempos
print(f"
Hacer el cálculo con listas de Python tarda {t_listas/t_ndarrays:.2f} veces más rápido que con ndarrays de NumPy")
	
	Copied

>_ Output

			
				Tiempo para realizar el producto escalar de dos listas de Python de dimensiones 1000x1000: 0.5234 ms
Tiempo para realizar el producto escalar de dos ndarrays de NumPy de dimensiones 1000x1000: 0.0017 ms
Hacer el cálculo con listas de Python tarda 316.66 veces más rápido que con ndarrays de NumPy

4. Matrices en NumPy

En NumPy una matriz es un objeto ndarray

	
		
			< >
			Input
		
		
			Python
			
		
	
	
		arr = np.array([1, 2, 3, 4, 5])
 
print(arr)
print(type(arr))
	
	Copied

>_ Output

			
				[1 2 3 4 5]
&lt;class 'numpy.ndarray'&gt;

4.1. Cómo crear matrices

Con el método array() se pueden crear ndarrays introduciendo listas de Python (como el ejemplo anterior) o tuplas

	
		
			< >
			Input
		
		
			Python
			
		
	
	
		arr = np.array((1, 2, 3, 4, 5))
 
print(arr)
print(type(arr))
	
	Copied

>_ Output

			
				[1 2 3 4 5]
&lt;class 'numpy.ndarray'&gt;

Con el método zeros() se pueden crear matrices llenas de ceros

	
		
			< >
			Input
		
		
			Python
			
		
	
	
		arr = np.zeros((3, 4))
 
print(arr)
	
	Copied

>_ Output

			
				[[0. 0. 0. 0.]
[0. 0. 0. 0.]
[0. 0. 0. 0.]]

El método zeros_like(A) devuelve una matriz con la misma forma que la matriz A, pero llena de ceros

	
		
			< >
			Input
		
		
			Python
			
		
	
	
		A = np.array((1, 2, 3, 4, 5))
arr = np.zeros_like(A)
 
print(arr)
	
	Copied

>_ Output

			
				[0 0 0 0 0]

Con el método ones() se pueden crear matrices llenas de unos

	
		
			< >
			Input
		
		
			Python
			
		
	
	
		arr = np.ones((4, 3))
 
print(arr)
	
	Copied

>_ Output

			
				[[1. 1. 1.]
[1. 1. 1.]
[1. 1. 1.]
[1. 1. 1.]]

El método ones_like(A) devuelve una matriz con la misma forma que la matriz A, pero llena de unos

	
		
			< >
			Input
		
		
			Python
			
		
	
	
		A = np.array((1, 2, 3, 4, 5))
arr = np.ones_like(A)
 
print(arr)
	
	Copied

>_ Output

			
				[1 1 1 1 1]

Con el método empty() se pueden crear matrices con las dimensiones que deseemos, pero inicializadas aleatoriamente

	
		
			< >
			Input
		
		
			Python
			
		
	
	
		arr = np.empty((6, 3))
 
print(arr)
	
	Copied

>_ Output

			
				[[4.66169180e-310 2.35541533e-312 2.41907520e-312]
[2.14321575e-312 2.46151512e-312 2.31297541e-312]
[2.35541533e-312 2.05833592e-312 2.22809558e-312]
[2.56761491e-312 2.48273508e-312 2.05833592e-312]
[2.05833592e-312 2.29175545e-312 2.07955588e-312]
[2.14321575e-312 0.00000000e+000 0.00000000e+000]]

El método empty_like(A) devuelve una matriz con la misma forma que la matriz A, pero inicializada aleatoriamente

	
		
			< >
			Input
		
		
			Python
			
		
	
	
		A = np.array((1, 2, 3, 4, 5))
arr = np.empty_like(A)
 
print(arr)
	
	Copied

>_ Output

			
				[4607182418800017408 4611686018427387904 4613937818241073152
4616189618054758400 4617315517961601024]

Con el método arange(start, stop, step) se pueden crear matrices en un rango determinado. Este método es similar al método range() de Python.

	
		
			< >
			Input
		
		
			Python
			
		
	
	
		arr = np.arange(10, 30, 5)
 
print(arr)
	
	Copied

>_ Output

			
				[10 15 20 25]

Cuando arange se usa con argumentos de coma flotante, generalmente no es posible predecir el número de elementos obtenidos, debido a que la precisión de la coma flotante es finita.

Por este motivo, suele ser mejor utilizar la función linspace(start, stop, n) que recibe como argumento la cantidad de elementos que queremos, en lugar del paso.

	
		
			< >
			Input
		
		
			Python
			
		
	
	
		arr = np.linspace(0, 2, 9)
 
print(arr)
	
	Copied

>_ Output

			
				[0.   0.25 0.5  0.75 1.   1.25 1.5  1.75 2.  ]

Por último, si queremos crear matrices con números aleatorios, podemos usar la función random.rand con una tupla con las dimensiones como parámetro

	
		
			< >
			Input
		
		
			Python
			
		
	
	
		arr = np.random.rand(2, 3)
 
print(arr)
	
	Copied

>_ Output

			
				[[0.32726085 0.65571767 0.73126697]
[0.91938206 0.9862451  0.95033649]]

4.2. Dimensiones de las matrices

En NumPy podemos crear matrices de cualquier dimensión. Para obtener la dimensión de un array utilizamos el método ndim

Matriz de dimensión 0, lo que equivaldría a un número

	
		
			< >
			Input
		
		
			Python
			
		
	
	
		arr = np.array(42)
 
print(arr)
print(arr.ndim)
	
	Copied

>_ Output

			
				42
0

Matriz de dimensión 1, lo que equivaldría a un vector

	
		
			< >
			Input
		
		
			Python
			
		
	
	
		arr = np.array([1, 2, 3, 4, 5])
 
print(arr)
print(arr.ndim)
	
	Copied

>_ Output

			
				[1 2 3 4 5]
1

Matriz de dimensión 2, lo que equivaldría a una matriz

	
		
			< >
			Input
		
		
			Python
			
		
	
	
		arr = np.array([[1, 2, 3, 4, 5],
                [6, 7, 8, 9, 10]])
 
print(arr)
print(arr.ndim)
	
	Copied

>_ Output

			
				[[ 1  2  3  4  5]
[ 6  7  8  9 10]]
2

Matriz de dimensión 3

	
		
			< >
			Input
		
		
			Python
			
		
	
	
		arr = np.array([
                [[1, 2, 3, 4, 5],
                [6, 7, 8, 9, 10]],
                
                [[11, 12, 13, 14, 15],
                [16, 17, 18, 19, 20]]
                ])
 
print(arr)
print(arr.ndim)
	
	Copied

>_ Output

			
				[[[ 1  2  3  4  5]
  [ 6  7  8  9 10]]
[[11 12 13 14 15]
  [16 17 18 19 20]]]
3

Matriz de dimensión N. A la hora de crear ndarrays se puede establecer el número de dimensiones mediante el parámetro ndim

	
		
			< >
			Input
		
		
			Python
			
		
	
	
		arr = np.array([1, 2, 3, 4, 5], ndmin=6)
 
print(arr)
print(arr.ndim)
	
	Copied

>_ Output

			
				[[[[[[1 2 3 4 5]]]]]]
6

4.3. Tamaño de las matrices

Si en vez de la dimensión de la matriz, queremos ver su tamaño, podemos usar el método shape

	
		
			< >
			Input
		
		
			Python
			
		
	
	
		arr = np.array([
                [[1, 2, 3, 4, 5],
                [6, 7, 8, 9, 10]],
                
                [[11, 12, 13, 14, 15],
                [16, 17, 18, 19, 20]]
                ])
 
print(arr.shape)
	
	Copied

>_ Output

			
				(2, 2, 5)

5. Tipo de datos

Los datos que pueden almacenar las matrices de NumPy son los siguientes:

i - entero
b - booleano
u - entero sin signo
f - flotante
c - Complejo flotante
m - Timedelta
M - DateTime
O - Objeto
S - string
U - Unicode string
V - Fragmento de memoria fijo para otro tipo (void)

Podemos comprobar el tipo de datos que tiene una matriz mediante dtype

	
		
			< >
			Input
		
		
			Python
			
		
	
	
		arr = np.array([1, 2, 3, 4])
print(arr.dtype)
 
arr = np.array(['apple', 'banana', 'cherry'])
print(arr.dtype)
	
	Copied

>_ Output

			
				int64
&lt;U6

También podemos crear matrices indicando el tipo de dato que queremos que tenga mediante dtype

	
		
			< >
			Input
		
		
			Python
			
		
	
	
		arr = np.array([1, 2, 3, 4], dtype='i')
print("Enteros:")
print(arr)
print(arr.dtype)
 
arr = np.array([1, 2, 3, 4], dtype='f')
print("
Float:")
print(arr)
print(arr.dtype)
 
arr = np.array([1, 2, 3, 4], dtype='f')
print("
Complejos:")
print(arr)
print(arr.dtype)
 
arr = np.array([1, 2, 3, 4], dtype='S')
print("
String:")
print(arr)
print(arr.dtype)
 
arr = np.array([1, 2, 3, 4], dtype='U')
print("
Unicode string:")
print(arr)
print(arr.dtype)
 
arr = np.array([1, 2, 3, 4], dtype='O')
print("
Objeto:")
print(arr)
print(arr.dtype)
	
	Copied

>_ Output

			
				Enteros:
[1 2 3 4]
int32
Float:
[1. 2. 3. 4.]
float32
Complejos:
[1. 2. 3. 4.]
float32
String:
[b'1' b'2' b'3' b'4']
|S1
Unicode string:
['1' '2' '3' '4']
&lt;U1
Objeto:
[1 2 3 4]
object

6. Operaciones matemáticas

6.1. Operaciones básicas

Las operaciones matriciales se realizan por elementos, por ejemplo, si sumamos dos matrices, se sumarán los elementos de cada matriz de la misma posición, al igual que se hace en la suma matemática de dos matrices

	
		
			< >
			Input
		
		
			Python
			
		
	
	
		A = np.array([1, 2, 3])
B = np.array([1, 2, 3])
 
print(f"Matriz A: tamaño {A.shape}
{A}
")
print(f"Matriz B: tamaño {B.shape}
{B}
")
 
C = A + B
print(f"Matriz C: tamaño {C.shape}
{C}
")
 
D = A - B
print(f"Matriz D: tamaño {D.shape}
{D}")
	
	Copied

>_ Output

			
				Matriz A: tamaño (3,)
[1 2 3]
Matriz B: tamaño (3,)
[1 2 3]
Matriz C: tamaño (3,)
[2 4 6]
Matriz D: tamaño (3,)
[0 0 0]

Sin embargo, si hacemos la multiplicación de dos matrices, también se hace la multiplicación de cada elemento de las matrices (producto escalar)

	
		
			< >
			Input
		
		
			Python
			
		
	
	
		A = np.array([[3, 5], [4, 1]])
B = np.array([[1, 2], [-3, 0]])
 
print(f"Matriz A: tamaño {A.shape}
{A}
")
print(f"Matriz B: tamaño {B.shape}
{B}
")
 
C = A * B
print(f"Matriz C: tamaño {C.shape}
{C}
")
	
	Copied

>_ Output

			
				Matriz A: tamaño (2, 2)
[[3 5]
[4 1]]
Matriz B: tamaño (2, 2)
[[ 1  2]
[-3  0]]
Matriz C: tamaño (2, 2)
[[  3  10]
[-12   0]]

Para hacer el producto matricial que se ha enseñado en matemáticas toda la vida hay que usar el operador @ o el método dot

	
		
			< >
			Input
		
		
			Python
			
		
	
	
		A = np.array([[3, 5], [4, 1], [6, -1]])
B = np.array([[1, 2, 3], [-3, 0, 4]])
 
print(f"Matriz A: tamaño {A.shape}
{A}
")
print(f"Matriz B: tamaño {B.shape}
{B}
")
 
C = A @ B
print(f"Matriz C: tamaño {C.shape}
{C}
")
 
D = A.dot(B)
print(f"Matriz D: tamaño {D.shape}
{D}")
	
	Copied

>_ Output

			
				Matriz A: tamaño (3, 2)
[[ 3  5]
[ 4  1]
[ 6 -1]]
Matriz B: tamaño (2, 3)
[[ 1  2  3]
[-3  0  4]]
Matriz C: tamaño (3, 3)
[[-12   6  29]
[  1   8  16]
[  9  12  14]]
Matriz D: tamaño (3, 3)
[[-12   6  29]
[  1   8  16]
[  9  12  14]]

Si en vez de crear una matriz nueva, se quiere modificar alguna existente se pueden usar los operadores +=, -= o *=

	
		
			< >
			Input
		
		
			Python
			
		
	
	
		A = np.array([[3, 5], [4, 1]])
B = np.array([[1, 2], [-3, 0]])
 
print(f"Matriz A: tamaño {A.shape}
{A}
")
print(f"Matriz B: tamaño {B.shape}
{B}
")
 
A += B
print(f"Matriz A tras suma: tamaño {A.shape}
{A}
")
 
A -= B
print(f"Matriz A tras resta: tamaño {A.shape}
{A}
")
 
A *= B
print(f"Matriz A tras multiplicación: tamaño {A.shape}
{A}
")
	
	Copied

>_ Output

			
				Matriz A: tamaño (2, 2)
[[3 5]
[4 1]]
Matriz B: tamaño (2, 2)
[[ 1  2]
[-3  0]]
Matriz A tras suma: tamaño (2, 2)
[[4 7]
[1 1]]
Matriz A tras resta: tamaño (2, 2)
[[3 5]
[4 1]]
Matriz A tras multiplicación: tamaño (2, 2)
[[  3  10]
[-12   0]]

Se pueden realizar operaciones sobre todos los elementos de una matriz, esto es gracias a una propiedad llamada broadcasting que veremos después más a fondo

	
		
			< >
			Input
		
		
			Python
			
		
	
	
		A = np.array([[3, 5], [4, 1]])
 
print(f"Matriz A: tamaño {A.shape}
{A}
")
 
B = A * 2
print(f"Matriz B: tamaño {B.shape}
{B}
")
 
C = A ** 2
print(f"Matriz C: tamaño {C.shape}
{C}
")
 
D = 2*np.sin(A)
print(f"Matriz D: tamaño {D.shape}
{D}")
	
	Copied

>_ Output

			
				Matriz A: tamaño (2, 2)
[[3 5]
[4 1]]
Matriz B: tamaño (2, 2)
[[ 6 10]
[ 8  2]]
Matriz C: tamaño (2, 2)
[[ 9 25]
[16  1]]
Matriz D: tamaño (2, 2)
[[ 0.28224002 -1.91784855]
[-1.51360499  1.68294197]]

6.2. Funciones sobre matrices

Como se puede ver en el último cálculo, NumPy ofrece operadores de funciones sobre matrices, hay un montón de funciones que se pueden realizar sobre matrices, matemáticas, lógicas, de álgebra lineal, etc. A continuación mostramos algunas

	
		
			< >
			Input
		
		
			Python
			
		
	
	
		A = np.array([[3, 5], [4, 1]])
 
print(f"A
{A}
")
 
print(f"exp(A)
{np.exp(A)}
")
print(f"sqrt(A)
{np.sqrt(A)}
")
print(f"cos(A)
{np.cos(A)}
")
	
	Copied

>_ Output

			
				A
[[3 5]
[4 1]]
exp(A)
[[ 20.08553692 148.4131591 ]
[ 54.59815003   2.71828183]]
sqrt(A)
[[1.73205081 2.23606798]
[2.         1.        ]]
cos(A)
[[-0.9899925   0.28366219]
[-0.65364362  0.54030231]]

Hay algunas funciones que devuelven información de las matrices, como la media

	
		
			< >
			Input
		
		
			Python
			
		
	
	
		A = np.array([[3, 5], [4, 1]])
 
print(f"A
{A}
")
 
print(f"A.mean()
{A.mean()}
")
	
	Copied

>_ Output

			
				A
[[3 5]
[4 1]]
A.mean()
3.25

Sin embargo, podemos obtener dicha información de cada eje mediante el atributo axis. Si este es 0, se hace sobre cada columna; mientras que si es 1, se hace sobre cada fila.

	
		
			< >
			Input
		
		
			Python
			
		
	
	
		A = np.array([[3, 5], [4, 1]])
 
print(f"A
{A}
")
 
print(f"A.mean() columnas
{A.mean(axis=0)}
")
print(f"A.mean() filas
{A.mean(axis=1)}
")
	
	Copied

>_ Output

			
				A
[[3 5]
[4 1]]
A.mean() columnas
[3.5 3. ]
A.mean() filas
[4.  2.5]

6.3. Broadcasting

Se pueden realizar operaciones matriciales con matrices de distintas dimensiones. En este caso, NumPy detectará esto y hará una proyección de la menor matriz hasta igualarla a la mayor

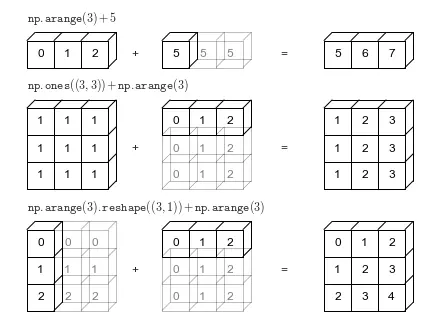
Esta es una gran cualidad de NumPy, que hace que se puedan realizar cálculos sobre matrices sin tener que preocuparse de igualar las dimensiones de estas

	
		
			< >
			Input
		
		
			Python
			
		
	
	
		A = np.array([1, 2, 3])
 
print(f"A
{A}
")
 
B = A + 5
 
print(f"B
{B}
")
	
	Copied

>_ Output

			
				A
[1 2 3]
B
[6 7 8]

	
		
			< >
			Input
		
		
			Python
			
		
	
	
		A = np.array([1, 2, 3])
B = np.ones((3,3))
 
print(f"A
{A}
")
print(f"B
{B}
")
 
C = A + B
 
print(f"C
{C}
")
	
	Copied

>_ Output

			
				A
[1 2 3]
B
[[1. 1. 1.]
[1. 1. 1.]
[1. 1. 1.]]
C
[[2. 3. 4.]
[2. 3. 4.]
[2. 3. 4.]]

	
		
			< >
			Input
		
		
			Python
			
		
	
	
		A = np.array([1, 2, 3])
B = np.array([[1], [2], [3]])
 
print(f"A
{A}
")
print(f"B
{B}
")
 
C = A + B
 
print(f"C
{C}
")
	
	Copied

>_ Output

			
				A
[1 2 3]
B
[[1]
[2]
[3]]
C
[[2 3 4]
[3 4 5]
[4 5 6]]

7. Indexado de matrices

El indexado de matrices se hace igual que con las listas de Python

	
		
			< >
			Input
		
		
			Python
			
		
	
	
		arr = np.array([1, 2, 3, 4, 5])
arr[3]
	
	Copied

>_ Output

En el caso de tener más de una dimensión, se debe indicar el índice en cada una de ellas

	
		
			< >
			Input
		
		
			Python
			
		
	
	
		arr = np.array([[1, 2, 3, 4, 5],
                [6, 7, 8, 9, 10]])
arr[1, 2]
	
	Copied

>_ Output

Se puede usar la indexación negativa

	
		
			< >
			Input
		
		
			Python
			
		
	
	
		arr[-1, -2]
	
	Copied

>_ Output

En caso de no indicar uno de los ejes, se considera que se quiere completo

	
		
			< >
			Input
		
		
			Python
			
		
	
	
		arr = np.array([[1, 2, 3, 4, 5],
                [6, 7, 8, 9, 10]])
arr[1]
	
	Copied

>_ Output

			
				array([ 6,  7,  8,  9, 10])

7.1. Porciones de matrices

A la hora de indexar, podemos quedarnos con partes de matrices al igual que se hacía con las listas de Python.

Recuerda que se hacía de la siguiente manera:

start:stop:step

Dónde el rango va desde el start (incluido) hasta el stop (sin incluir) con un paso de step

Si step no se indica, por defecto es 1

Por ejemplo, si queremos items de la segunda fila y de la segunda a la cuarta columna:

Seleccionamos la segunda fila con un 1 (ya que se empieza a contar desde 0)
Seleccionamos de la segunda a la cuarta fila mediante 1:4, el 1 para indicar la segunda columna y el 4 para indicar la quinta (ya que el segundo número indica la columna en la que se termina sin incluir esta columna). Los dos números teniendo en cuenta que se empieza a contar desde 0

	
		
			< >
			Input
		
		
			Python
			
		
	
	
		print(arr)
print(arr[1, 1:4])
	
	Copied

>_ Output

			
				[[ 1  2  3  4  5]
[ 6  7  8  9 10]]
[7 8 9]

Podemos coger desde una posición hasta el final

	
		
			< >
			Input
		
		
			Python
			
		
	
	
		arr[1, 2:]
	
	Copied

>_ Output

			
				array([ 8,  9, 10])

Desde el inicio hasta una posición

	
		
			< >
			Input
		
		
			Python
			
		
	
	
		arr[1, :3]
	
	Copied

>_ Output

			
				array([6, 7, 8])

Establecer el rango con números negativos

	
		
			< >
			Input
		
		
			Python
			
		
	
	
		arr[1, -3:-1]
	
	Copied

>_ Output

			
				array([8, 9])

Elegir el paso

	
		
			< >
			Input
		
		
			Python
			
		
	
	
		arr[1, 1:4:2]
	
	Copied

>_ Output

			
				array([7, 9])

7.2. Iteración sobre matrices

La iteración sobre matrices multidimensionales se realiza con respecto al primer eje

	
		
			< >
			Input
		
		
			Python
			
		
	
	
		M = np.array( [[[ 0, 1, 2],
                [ 10, 12, 13]],
               [[100,101,102],
                [110,112,113]]])
 
print(f'Matriz de dimensión: {M.shape}
')
 
i = 0
for fila in M:
  print(f'Fila {i}: {fila}')
  i += 1
	
	Copied

>_ Output

			
				Matriz de dimensión: (2, 2, 3)
Fila 0: [[ 0  1  2]
[10 12 13]]
Fila 1: [[100 101 102]
[110 112 113]]

Sin embargo, si lo que queremos es iterar por cada ítem, podemos usar el método 'flat'

	
		
			< >
			Input
		
		
			Python
			
		
	
	
		i = 0
for fila in M.flat:
  print(f'Elemento {i}: {fila}')
  i += 1
	
	Copied

>_ Output

			
				Elemento 0: 0
Elemento 1: 1
Elemento 2: 2
Elemento 3: 10
Elemento 4: 12
Elemento 5: 13
Elemento 6: 100
Elemento 7: 101
Elemento 8: 102
Elemento 9: 110
Elemento 10: 112
Elemento 11: 113

8. Copia de matrices

En NumPy tenemos dos maneras de copiar matrices: mediante copy, que realiza una copia nueva de la matriz, y mediante view, que realiza una vista de la matriz original.

La copia es propietaria de los datos y cualquier cambio realizado en la copia no afectará a la matriz original, y cualquier cambio realizado en la matriz original no afectará a la copia.

La vista no es propietaria de los datos y cualquier cambio realizado en la copia afectará a la matriz original, y cualquier cambio realizado en la matriz original afectará a la copia.

8.1. Copy

	
		
			< >
			Input
		
		
			Python
			
		
	
	
		arr = np.array([1, 2, 3, 4, 5])
copy_arr = arr.copy()
arr[0] = 42
copy_arr[1] = 43
 
print(f'Original: {arr}')
print(f'Copia:    {copy_arr}')
	
	Copied

>_ Output

			
				Original: [42  2  3  4  5]
Copia:    [ 1 43  3  4  5]

8.2. View

	
		
			< >
			Input
		
		
			Python
			
		
	
	
		arr = np.array([1, 2, 3, 4, 5])
view_arr = arr.view()
arr[0] = 42
view_arr[1] = 43
 
print(f'Original: {arr}')
print(f'Vista:    {view_arr}')
	
	Copied

>_ Output

			
				Original: [42 43  3  4  5]
Vista:    [42 43  3  4  5]

8.3. Propietario de los datos

Ante la duda de si tenemos una copia o una vista, podemos usar base

	
		
			< >
			Input
		
		
			Python
			
		
	
	
		arr = np.array([1, 2, 3, 4, 5])
 
copy_arr = arr.copy()
view_arr = arr.view()
 
print(copy_arr.base)
print(view_arr.base)
	
	Copied

>_ Output

			
				None
[1 2 3 4 5]

9. Forma de las matrices

Podemos saber la forma que tiene la matriz mediante el método shape. Este nos devolverá una tupla, el tamaño de la tupla representa las dimensiones de la matriz, en cada elemento de la tupla se indica el número de ítems en cada una de las dimensiones de la matriz

	
		
			< >
			Input
		
		
			Python
			
		
	
	
		arr = np.array([
                [[1, 2, 3, 4, 5],
                [6, 7, 8, 9, 10]],
                
                [[11, 12, 13, 14, 15],
                [16, 17, 18, 19, 20]]
                ])
 
print(arr)
print(arr.shape)
	
	Copied

>_ Output

			
				[[[ 1  2  3  4  5]
  [ 6  7  8  9 10]]
[[11 12 13 14 15]
  [16 17 18 19 20]]]
(2, 2, 5)

9.1. Reshape

Podemos cambiar la forma de las matrices a la que queramos mediante el método reshape.

Por ejemplo, la matriz anterior, que tiene una forma de (2, 2, 4). Podemos pasarla a (5, 4)

	
		
			< >
			Input
		
		
			Python
			
		
	
	
		arr_reshape = arr.reshape(5, 4)
 
print(arr_reshape)
print(arr_reshape.shape)
	
	Copied

>_ Output

			
				[[ 1  2  3  4]
[ 5  6  7  8]
[ 9 10 11 12]
[13 14 15 16]
[17 18 19 20]]
(5, 4)

Hay que tener en cuenta que para redimensionar las matrices el número de ítems de la nueva forma tiene que tener el mismo número de ítems de la primera forma

Es decir, en el ejemplo anterior, la primera matriz tenía 20 ítems (2x2x4), y la nueva matriz tiene 20 ítems (5x4). Lo que no podemos es redimensionarla a una matriz de tamaño (3, 4), ya que en total habría 12 ítems

	
		
			< >
			Input
		
		
			Python
			
		
	
	
		arr_reshape = arr.reshape(3, 4)
	
	Copied

>_ Output

			
				---------------------------------------------------------------------------ValueError                                Traceback (most recent call last)&lt;ipython-input-12-29e85875d1df&gt; in &lt;module&gt;()
----&gt; 1 arr_reshape = arr.reshape(3, 4)
ValueError: cannot reshape array of size 20 into shape (3,4)

9.2. Dimensión desconocida

En el caso que queramos cambiar la forma de una matriz y una de las dimensiones nos dé igual, o no la conozcamos, podemos hacer que NumPy la calcule por nosotros introduciendo un -1 como parámetro

	
		
			< >
			Input
		
		
			Python
			
		
	
	
		arr = np.array([
                [[1, 2, 3, 4, 5],
                [6, 7, 8, 9, 10]],
                
                [[11, 12, 13, 14, 15],
                [16, 17, 18, 19, 20]]
                ])
 
arr_reshape = arr.reshape(2, -1)
 
print(arr_reshape)
print(arr_reshape.shape)
	
	Copied

>_ Output

			
				[[ 1  2  3  4  5  6  7  8  9 10]
[11 12 13 14 15 16 17 18 19 20]]
(2, 10)

Hay que tener en cuenta que no se puede poner cualquier número en las dimensiones conocidas. El número de ítems de la matriz original tiene que ser un múltiplo de las dimensiones conocidas.

En el ejemplo anterior, la matriz tiene 20 ítems, que es múltiplo de 2, dimensión conocida introducida. No se hubiera podido poner un 3 como dimensión conocida, ya que 20 no es múltiplo de 3, y no habría ningún número que se pueda poner en la dimensión desconocida que haga que en total haya 20 ítems.

9.3. Aplanamiento de matrices

Podemos aplanar las matrices, es decir, pasarlas a una sola dimensión mediante reshape(-1). De esta manera, tenga las dimensiones que tenga la matriz original, la nueva siempre tendrá una sola dimensión

	
		
			< >
			Input
		
		
			Python
			
		
	
	
		arr = np.array([
                [[1, 2, 3, 4, 5],
                [6, 7, 8, 9, 10]],
                
                [[11, 12, 13, 14, 15],
                [16, 17, 18, 19, 20]]
                ])
 
arr_flatten = arr.reshape(-1)
 
print(arr_flatten)
print(arr_flatten.shape)
	
	Copied

>_ Output

			
				[ 1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17 18 19 20]
(20,)

Otra forma de aplanar una matriz es mediante el método ravel()

	
		
			< >
			Input
		
		
			Python
			
		
	
	
		arr = np.array([
                [[1, 2, 3, 4, 5],
                [6, 7, 8, 9, 10]],
                
                [[11, 12, 13, 14, 15],
                [16, 17, 18, 19, 20]]
                ])
 
arr_flatten = arr.ravel()
 
print(arr_flatten)
print(arr_flatten.shape)
	
	Copied

>_ Output

			
				[ 1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17 18 19 20]
(20,)

9.4. Matriz traspuesta

Se puede obtener la transpuesta de una matriz mediante el método T. Hacer la transpuesta de una matriz es intercambiar las filas y las columnas de la matriz, en la siguiente imagen se ve un ejemplo que lo aclara más

	
		
			< >
			Input
		
		
			Python
			
		
	
	
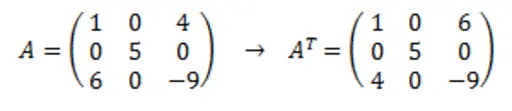
		arr = np.array([[1, 0, 4],
                [0, 5, 0],
                [6, 0, -9]])
 
arr_t = arr.T
 
print(arr_t)
print(arr_t.shape)
	
	Copied

>_ Output

			
				[[ 1  0  6]
[ 0  5  0]
[ 4  0 -9]]
(3, 3)

10. Apilado de matrices

10.1. Apilamiento vertical

Se pueden apilar matrices verticalmente (uniendo filas) mediante el método vstack()

	
		
			< >
			Input
		
		
			Python
			
		
	
	
		a = np.array([[1, 1, 1],
              [2, 2, 2],
              [3, 3, 3]])
 
b = np.array([[4, 4, 4],
              [5, 5, 5],
              [6, 6, 6]])
 
c = np.vstack((a,b))
c
	
	Copied

>_ Output

			
				array([[1, 1, 1],
       [2, 2, 2],
       [3, 3, 3],
       [4, 4, 4],
       [5, 5, 5],
       [6, 6, 6]])

Si se tienen matrices de más de 2 dimensiones, vstack() apilará a lo largo de la primera dimensión

	
		
			< >
			Input
		
		
			Python
			
		
	
	
		a = np.array([
                [[1, 1],
                [2, 2]],
                
                [[3, 3],
                [4, 4]]
                ])
 
b = np.array([
                [[5, 5],
                [6, 6]],
                
                [[7, 7],
                [8, 8]]
                ])
 
c = np.vstack((a,b))
c
	
	Copied

>_ Output

			
				array([[[1, 1],
        [2, 2]],
       [[3, 3],
        [4, 4]],
       [[5, 5],
        [6, 6]],
       [[7, 7],
        [8, 8]]])

10.2. Apilamiento horizontal

Se pueden apilar matrices horizontalmente (uniendo columnas) mediante el método hstack()

	
		
			< >
			Input
		
		
			Python
			
		
	
	
		a = np.array([[1, 2, 3],
              [1, 2, 3],
              [1, 2, 3]])
 
b = np.array([[4, 5, 6],
              [4, 5, 6],
              [4, 5, 6]])
 
c = np.hstack((a,b))
c
	
	Copied

>_ Output

			
				array([[1, 2, 3, 4, 5, 6],
       [1, 2, 3, 4, 5, 6],
       [1, 2, 3, 4, 5, 6]])

Si se tienen matrices de más de 2 dimensiones, hstack() apilará a lo largo de la segunda dimensión

	
		
			< >
			Input
		
		
			Python
			
		
	
	
		a = np.array([
                [[1, 1],
                [2, 2]],
                
                [[3, 3],
                [4, 4]]
                ])
 
b = np.array([
                [[5, 5],
                [6, 6]],
                
                [[7, 7],
                [8, 8]]
                ])
 
c = np.hstack((a,b))
c
	
	Copied

>_ Output

			
				array([[[1, 1],
        [2, 2],
        [5, 5],
        [6, 6]],
       [[3, 3],
        [4, 4],
        [7, 7],
        [8, 8]]])

Otra manera de agregar columnas a una matriz es mediante el método column_stack()

	
		
			< >
			Input
		
		
			Python
			
		
	
	
		a = np.array([[1, 2, 3],
              [1, 2, 3],
              [1, 2, 3]])
 
b = np.array([4, 4, 4])
 
c = np.column_stack((a,b))
c
	
	Copied

>_ Output

			
				array([[1, 2, 3, 4],
       [1, 2, 3, 4],
       [1, 2, 3, 4]])

10.3. Apilamiento en profundidad

Se pueden apilar matrices en profundidad (tercera dimensión) mediante el método dstack()

	
		
			< >
			Input
		
		
			Python
			
		
	
	
		a = np.array([
                [[1, 1],
                [2, 2]],
                
                [[3, 3],
                [4, 4]]
                ])
 
b = np.array([
                [[1, 1],
                [2, 2]],
                
                [[3, 3],
                [4, 4]]
                ])
 
c = np.dstack((a,b))
print(f"c: {c}
")
print(f"a.shape: {a.shape}, b.shape: {b.shape}, c.shape: {c.shape}")
	
	Copied

>_ Output

			
				c: [[[1 1 1 1]
  [2 2 2 2]]
[[3 3 3 3]
  [4 4 4 4]]]
a.shape: (2, 2, 2), b.shape: (2, 2, 2), c.shape: (2, 2, 4)

Si se tienen matrices de más de 4 dimensiones dstack() apilirá a lo largo de la tercera dimensión

	
		
			< >
			Input
		
		
			Python
			
		
	
	
		a = np.array([1, 2, 3, 4, 5], ndmin=4)
 
b = np.array([1, 2, 3, 4, 5], ndmin=4)
 
c = np.dstack((a,b))
print(f"a.shape: {a.shape}, b.shape: {b.shape}, c.shape: {c.shape}")
	
	Copied

>_ Output

			
				a.shape: (1, 1, 1, 5), b.shape: (1, 1, 1, 5), c.shape: (1, 1, 2, 5)

10.3. Apilamiento personalizado

Mediante el método concatenate() se puede elegir el eje en el que se quieran apilar las matrices

	
		
			< >
			Input
		
		
			Python
			
		
	
	
		a = np.array([
                [[1, 1],
                [2, 2]],
                
                [[3, 3],
                [4, 4]]
                ])
 
b = np.array([
                [[5, 5],
                [6, 6]],
                
                [[7, 7],
                [8, 8]]
                ])
 
conc0 = np.concatenate((a,b), axis=0) # concatenamiento en el primer eje
conc1 = np.concatenate((a,b), axis=1) # concatenamiento en el segundo eje
conc2 = np.concatenate((a,b), axis=2) # concatenamiento en el tercer eje
print(f"conc0: {conc0}
")
print(f"conc1: {conc1}
")
print(f"conc2: {conc2}")
	
	Copied

>_ Output

			
				conc0: [[[1 1]
  [2 2]]
[[3 3]
  [4 4]]
[[5 5]
  [6 6]]
[[7 7]
  [8 8]]]
conc1: [[[1 1]
  [2 2]
  [5 5]
  [6 6]]
[[3 3]
  [4 4]
  [7 7]
  [8 8]]]
conc2: [[[1 1 5 5]
  [2 2 6 6]]
[[3 3 7 7]
  [4 4 8 8]]]

11. Dividir matrices

11.1. Dividir verticalmente

Se pueden dividir matrices verticalmente (separando filas) mediante el método vsplit()

	
		
			< >
			Input
		
		
			Python
			
		
	
	
		a = np.array([[1.1, 1.2, 1.3, 1.4],
              [2.1, 2.2, 2.3, 2.4],
              [3.1, 3.2, 3.3, 3.4],
              [4.1, 4.2, 4.3, 4.4]])
 
[a1, a2] = np.vsplit(a, 2)
print(f"a1: {a1}
")
print(f"a2: {a2}")
	
	Copied

>_ Output

			
				a1: [[1.1 1.2 1.3 1.4]
[2.1 2.2 2.3 2.4]]
a2: [[3.1 3.2 3.3 3.4]
[4.1 4.2 4.3 4.4]]

Si se tienen matrices de más de 2 dimensiones, vsplit() dividirá a lo largo de la primera dimensión.

	
		
			< >
			Input
		
		
			Python
			
		
	
	
		a = np.array([
                [[1, 1],
                [2, 2]],
                
                [[3, 3],
                [4, 4]]
                ])
 
[a1, a2] = np.vsplit(a, 2)
print(f"a1: {a1}
")
print(f"a2: {a2}")
	
	Copied

>_ Output

			
				a1: [[[1 1]
  [2 2]]]
a2: [[[3 3]
  [4 4]]]

11.2. Dividir horizontalmente

Se pueden dividir matrices horizontalmente (separando columnas) mediante el método hsplit()

	
		
			< >
			Input
		
		
			Python
			
		
	
	
		a = np.array([[1.1, 1.2, 1.3, 1.4],
              [2.1, 2.2, 2.3, 2.4],
              [3.1, 3.2, 3.3, 3.4],
              [4.1, 4.2, 4.3, 4.4]])
 
[a1, a2] = np.hsplit(a, 2)
print(f"a1: {a1}
")
print(f"a2: {a2}")
	
	Copied

>_ Output

			
				a1: [[1.1 1.2]
[2.1 2.2]
[3.1 3.2]
[4.1 4.2]]
a2: [[1.3 1.4]
[2.3 2.4]
[3.3 3.4]
[4.3 4.4]]

Si se tienen matrices de más de 2 dimensiones, hsplit() dividirá a lo largo de la segunda dimensión

	
		
			< >
			Input
		
		
			Python
			
		
	
	
		a = np.array([
                [[1, 1],
                [2, 2]],
                
                [[3, 3],
                [4, 4]]
                ])
 
[a1, a2] = np.hsplit(a, 2)
print(f"a1: {a1}
")
print(f"a2: {a2}")
	
	Copied

>_ Output

			
				a1: [[[1 1]]
[[3 3]]]
a2: [[[2 2]]
[[4 4]]]

11.3. Dividir de manera personalizada

Mediante el método array_split() se puede elegir el eje en el que se quieren dividir las matrices

	
		
			< >
			Input
		
		
			Python
			
		
	
	
		a = np.array([
                [[1, 1],
                [2, 2]],
                
                [[3, 3],
                [4, 4]]
                ])
 
[a1_eje0, a2_eje0] = np.array_split(a, 2, axis=0)
[a1_eje1, a2_eje1] = np.array_split(a, 2, axis=1)
[a1_eje2, a2_eje2] = np.array_split(a, 2, axis=2)
 
print(f"a1_eje0: {a1_eje0}
")
print(f"a2_eje0: {a2_eje0}

")
 
print(f"a1_eje1: {a1_eje1}
")
print(f"a2_eje1: {a2_eje1}

")
 
print(f"a1_eje2: {a1_eje2}
")
print(f"a2_eje2: {a2_eje2}")
	
	Copied

>_ Output

			
				a1_eje0: [[[1 1]
  [2 2]]]
a2_eje0: [[[3 3]
  [4 4]]]
a1_eje1: [[[1 1]]
[[3 3]]]
a2_eje1: [[[2 2]]
[[4 4]]]
a1_eje2: [[[1]
  [2]]
[[3]
  [4]]]
a2_eje2: [[[1]
  [2]]
[[3]
  [4]]]

12. Búsqueda en matrices

Si se quiere buscar un valor dentro de una matriz, se puede usar el método where() que devuelve las posiciones donde la matriz tiene el valor que estamos buscando

	
		
			< >
			Input
		
		
			Python
			
		
	
	
		arr = np.array([1, 2, 3, 4, 5, 4, 4])
 
ids = np.where(arr == 4)
ids
	
	Copied

>_ Output

			
				(array([3, 5, 6]),)

Se pueden usar funciones para buscar, por ejemplo, si queremos buscar en qué posiciones los valores son pares

	
		
			< >
			Input
		
		
			Python
			
		
	
	
		arr = np.array([1, 2, 3, 4, 5, 6, 7, 8])
 
ids = np.where(arr%2)
ids
	
	Copied

>_ Output

			
				(array([0, 2, 4, 6]),)

13. Ordenar matrices

Mediante el método sort() podemos ordenar matrices

	
		
			< >
			Input
		
		
			Python
			
		
	
	
		arr = np.array([3, 2, 0, 1])
 
arr_ordenado = np.sort(arr)
arr_ordenado
	
	Copied

>_ Output

			
				array([0, 1, 2, 3])

Si lo que tenemos son strings, los ordena alfabéticamente

	
		
			< >
			Input
		
		
			Python
			
		
	
	
		arr = np.array(['banana', 'apple', 'cherry'])
 
arr_ordenado = np.sort(arr)
arr_ordenado
	
	Copied

>_ Output

			
				array(['apple', 'banana', 'cherry'], dtype='&lt;U6')

Y las matrices de booleanos también las ordena

	
		
			< >
			Input
		
		
			Python
			
		
	
	
		arr = np.array([True, False, True])
 
arr_ordenado = np.sort(arr)
arr_ordenado
	
	Copied

>_ Output

			
				array([False,  True,  True])

Si se tienen matrices de más de una dimensión, las ordena por dimensiones, es decir, si se tiene una matriz de 2 dimensiones, ordena los números de la primera fila entre ellos y los de la segunda fila entre ellos

	
		
			< >
			Input
		
		
			Python
			
		
	
	
		arr = np.array([[3, 2, 4], [5, 0, 1]])
 
arr_ordenado = np.sort(arr)
arr_ordenado
	
	Copied

>_ Output

			
				array([[2, 3, 4],
       [0, 1, 5]])

Por defecto ordena siempre con respecto a las filas, pero si se quiere que ordene con respecto a otra dimensión, se tiene que especificar mediante la variable axis

	
		
			< >
			Input
		
		
			Python
			
		
	
	
		arr = np.array([[3, 2, 4], [5, 0, 1]])
 
arr_ordenado0 = np.sort(arr, axis=0) # Se ordena con respecto a la primera dimensión
arr_ordenado1 = np.sort(arr, axis=1) # Se ordena con respecto a la segunda dimensión
 
print(f"arr_ordenado0: {arr_ordenado0}
")
print(f"arr_ordenado1: {arr_ordenado1}
")
	
	Copied

>_ Output

			
				arr_ordenado0: [[3 0 1]
[5 2 4]]
arr_ordenado1: [[2 3 4]
[0 1 5]]

14. Filtros en matrices

NumPy ofrece la posibilidad de buscar ciertos elementos de una matriz y crear una nueva

Esto lo hace creando una matriz de índices booleanos, es decir, crea una nueva matriz que indica cuáles posiciones nos quedamos de la matriz y cuáles no

Veamos un ejemplo de una matriz de índices booleanos

	
		
			< >
			Input
		
		
			Python
			
		
	
	
		arr = np.array([37, 85, 12, 45, 69, 22])
 
indices_booleanos = [False, False, True, False, False, True]
 
arr_filter = arr[indices_booleanos]
 
print(f"Array original: {arr}")
print(f"indices booleanos: {indices_booleanos}")
print(f"Array filtrado: {arr_filter}")
	
	Copied

>_ Output

			
				Array original: [37 85 12 45 69 22]
indices booleanos: [False, False, True, False, False, True]
Array filtrado: [12 22]

Como se puede ver, el array filtrado (arr_filtr), solo se ha quedado del array original (arr) con los elementos que coinciden con aquellos en los que el array indices_booleanos vale True

Otra cosa que podemos ver es que solo se ha quedado con los elementos pares, por lo que ahora pasaremos a ver cómo se hace para quedarse con los elementos pares de una matriz, sin tener que hacerlo a mano como lo hemos hecho en el ejemplo anterior

	
		
			< >
			Input
		
		
			Python
			
		
	
	
		arr = np.array([[1, 2, 3, 4, 5],
                [6, 7, 8, 9, 10]])
 
indices_booleanos = arr % 2 == 0
 
arr_filter = arr[indices_booleanos]
 
print(f"Array original: {arr}
")
print(f"indices booleanos: {indices_booleanos}
")
print(f"Array filtrado: {arr_filter}")
	
	Copied

>_ Output

			
				Array original: [[ 1  2  3  4  5]
[ 6  7  8  9 10]]
indices booleanos: [[False  True False  True False]
[ True False  True False  True]]
Array filtrado: [ 2  4  6  8 10]

Seguir leyendo

Deep Research con LangGraph: Crea un Asistente de IA para Investigar Automáticamente

Aprende cómo funcionan las redes neuronales desde cero con un ejemplo práctico de regresión lineal. Tutorial paso a paso que explica neuronas artificiales, inicialización de parámetros, funciones de pérdida y error cuadrático medio (ECM) con código Python.

Elicitación MCP: Implementar Elicitación en Servidores con FastMCP y Python

Aprende a implementar elicitación en servidores MCP (Model Context Protocol) con FastMCP. Tutorial completo paso a paso ...

MCP Durability: Servidor y Cliente con Persistencia para Tareas de Larga Duración

Aprende a crear un servidor y cliente MCP con durabilidad para tareas de larga duración. Tutorial completo sobre Model C...

Últimos posts -->

¿Has visto estos proyectos?

Gymnasia

Horeca chatbot

Naviground

Ver todos los proyectos -->

>_ Disponible para proyectos

¿Tienes un proyecto con IA?

Hablemos.

maximofn@gmail.com

Especialista en Machine Learning e Inteligencia Artificial. Desarrollo soluciones con IA generativa, agentes inteligentes y modelos personalizados.

Escríbeme LinkedIn

¿Quieres ver alguna charla?

Agentes del Mañana: Descifrando los Enigmas de Planificación, UX y Memoria

Los agentes IA, impulsados por LLMs, prometen transformar aplicaciones. Pero, ¿son hoy simples ejecutores o futuros colaboradores inteligentes? Para a...

Crea tu propio Apple intelligence

Aprende a crear un sistema de IA para ejecutar eficientemente en un dispositivo

Últimas charlas -->

¿Quieres mejorar con estos tips?

o1 prompt engineering

Crear mejores prompts para o1 siguiendo un ejemplo

Memory profiler

Ver el uso de memoria de un script

DataLoader con pin_memory y num_workers

Aumentar el rendimiento de DataLoader con pin_memory y num_workers

Últimos tips -->

Usa esto en local

Los espacios de Hugging Face nos permite ejecutar modelos con demos muy sencillas, pero ¿qué pasa si la demo se rompe? O si el usuario la elimina? Por ello he creado contenedores docker con algunos espacios interesantes, para poder usarlos de manera local, pase lo que pase. De hecho, es posible que si pinchas en alún botón de ver proyecto te lleve a un espacio que no funciona.

Flow edit

FLUX.1-RealismLora

token_hmr

Ver todos los contenedores -->

>_ Disponible para proyectos

¿Tienes un proyecto con IA?

Hablemos.

maximofn@gmail.com

Especialista en Machine Learning e Inteligencia Artificial. Desarrollo soluciones con IA generativa, agentes inteligentes y modelos personalizados.

Escríbeme LinkedIn

¿Quieres entrenar tu modelo con estos datasets?

short-jokes-dataset

HuggingFace

Dataset de chistes en inglés

Uso: Fine-tuning de modelos de generación de texto humorístico

231K filas 2 columnas 45 MB

Ver en HuggingFace →

opus100

HuggingFace

Dataset con traducciones de inglés a español

Uso: Entrenamiento de modelos de traducción inglés-español

1M filas 2 columnas 210 MB

Ver en HuggingFace →

netflix_titles

HuggingFace

Dataset con películas y series de Netflix

Uso: Análisis de catálogo de Netflix y sistemas de recomendación

8.8K filas 12 columnas 3.5 MB

Ver en HuggingFace →

Ver más datasets -->

1. Resumen

2. ¿Qué es NumPy?

2.1. NumPy como np

3. Velocidad de NumPy

4. Matrices en NumPy

4.1. Cómo crear matrices

4.2. Dimensiones de las matrices

4.3. Tamaño de las matrices

5. Tipo de datos

6. Operaciones matemáticas

6.1. Operaciones básicas

6.2. Funciones sobre matrices

6.3. Broadcasting

7. Indexado de matrices

7.1. Porciones de matrices

7.2. Iteración sobre matrices

8. Copia de matrices

8.1. Copy

8.2. View

8.3. Propietario de los datos

9. Forma de las matrices

9.1. Reshape

9.2. Dimensión desconocida

9.3. Aplanamiento de matrices

9.4. Matriz traspuesta

10. Apilado de matrices

10.1. Apilamiento vertical

10.2. Apilamiento horizontal

10.3. Apilamiento en profundidad

10.3. Apilamiento personalizado

11. Dividir matrices

11.1. Dividir verticalmente

11.2. Dividir horizontalmente

11.3. Dividir de manera personalizada

12. Búsqueda en matrices

13. Ordenar matrices

14. Filtros en matrices

Seguir leyendo

Deep Research con LangGraph: Crea un Asistente de IA para Investigar Automáticamente

Elicitación MCP: Implementar Elicitación en Servidores con FastMCP y Python

MCP Durability: Servidor y Cliente con Persistencia para Tareas de Larga Duración

¿Has visto estos proyectos?

¿Tienes un proyecto con IA?

¿Quieres ver alguna charla?

Agentes del Mañana: Descifrando los Enigmas de Planificación, UX y Memoria

Crea tu propio Apple intelligence

¿Quieres mejorar con estos tips?

o1 prompt engineering

Memory profiler

DataLoader con pin_memory y num_workers

Usa esto en local

¿Tienes un proyecto con IA?

¿Quieres entrenar tu modelo con estos datasets?

short-jokes-dataset

opus100

netflix_titles

2.1. NumPy como `np`