Transformers - de cima para baixo

Nesta postagem, veremos como os Transformers funcionam de cima para baixo.

Este caderno foi traduzido automaticamente para torná-lo acessível a mais pessoas, por favor me avise se você vir algum erro de digitação..

Transformador como uma caixa preta

A arquitetura do transformador foi criada para o problema de tradução, portanto, vamos explicá-la para esse problema.

Imagine o transformador como uma caixa preta, que recebe uma frase em um idioma e produz a mesma frase traduzida em outro idioma.

Transformador - caixa preta] (https://pub-fb664c455eca46a2ba762a065ac900f7.r2.dev/Transformer-black-box.webp)

Tokenização

Mas, como vimos na postagem tokens, os modelos de linguagem não entendem as palavras como nós, eles precisam de números para poder realizar operações. Portanto, a sentença original do idioma precisa ser convertida em tokens por um tokenizador e, na saída, precisamos de um detokenizador para converter os tokens de saída em palavras.

Assim, o tokenizador cria uma sequência de tokens $n_{input-tokens}$ e o destokenizador recebe uma sequência de tokens $n_{output-tokens}$.

Embeddings de entrada

Na postagem embeddings, vimos que os embeddings são uma forma de representar palavras em um espaço vetorial. Portanto, os tokens de entrada são passados por uma camada de embeddings para convertê-los em vetores.

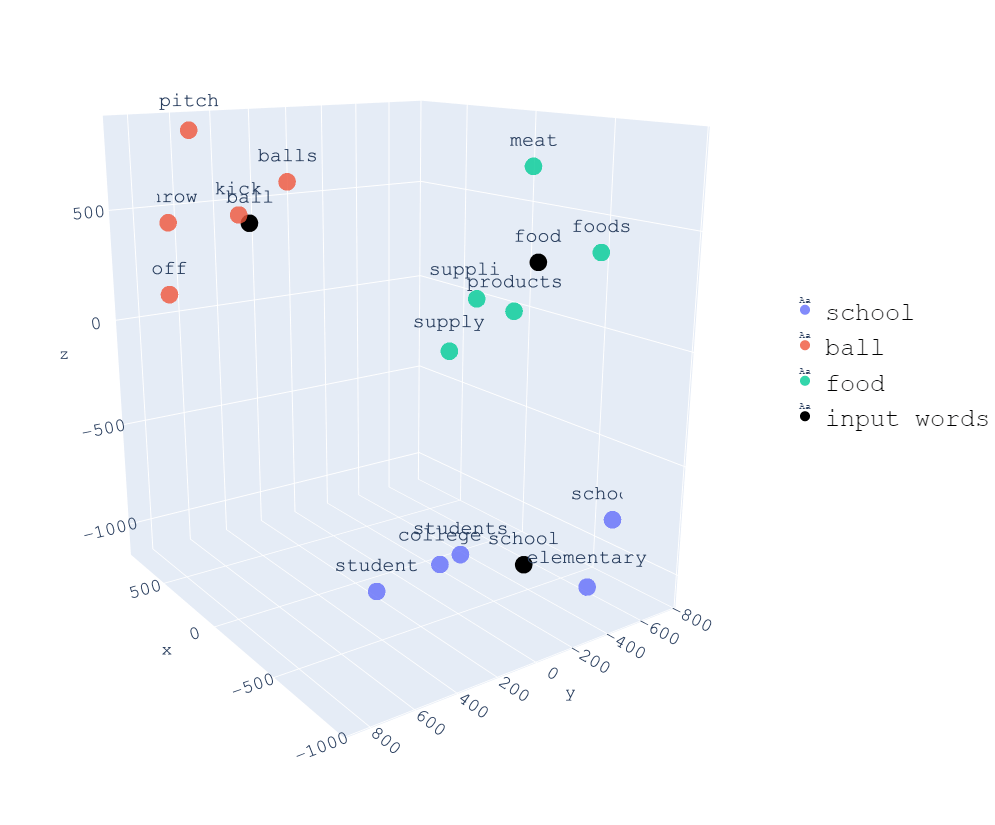
Em um resumo rápido, o processo de incorporação consiste em converter uma sequência de números (tokens) em uma sequência de vetores. Assim, é criado um novo espaço vetorial no qual as palavras que têm semelhança semântica estarão muito próximas.

Se tivéssemos $n_{input-tokens}$ tokens, agora teríamos $n_{input-tokens}$ vetores. Cada um desses vetores tem um comprimento de $d_{model}$. Ou seja, cada token é convertido em um vetor que representa esse token em um espaço vetorial de dimensões $d_{model}$$. Portanto, depois de passar pela camada de incorporação, a sequência de tokens $n_{input-tokens}$ se torna uma matriz de ($n_{input-tokens}$$ x $d_{model}$).

Transformador - caixa preta - embeddings de entrada](https://pub-fb664c455eca46a2ba762a065ac900f7.r2.dev/Transformer-black-box-input-embeddings.webp)

Codificador - decodificador

Vimos o transformador atuando como uma caixa preta, mas, na realidade, o transformador é uma arquitetura composta de duas partes, um codificador e um decodificador.

Transformador - codificador-decodificador] (https://pub-fb664c455eca46a2ba762a065ac900f7.r2.dev/Transformer-encoder-decoder.png)

O codificador é responsável por comprimir as informações da frase de entrada, criando um espaço latente no qual as informações da frase de entrada são comprimidas. Em seguida, essas informações comprimidas entram no decodificador, que sabe como converter essas informações comprimidas em uma frase do idioma de saída.

E como o decodificador converte essas informações compactadas em uma frase no idioma de saída? Bem, token por token. Para entender melhor, vamos esquecer os tokens de saída por um momento e imaginar que temos a seguinte arquitetura

Transformador - codificador-decodificador (sem destokenizador)](https://pub-fb664c455eca46a2ba762a065ac900f7.r2.dev/Transformer-encoder-decoder-no-detokenizer.webp)

Ou seja, a frase do idioma original é convertida em tokens, esses tokens são convertidos em embeddings, que entram no codificador, o codificador comprime as informações, o decodificador as pega e as converte em palavras do idioma de saída.

Assim, o decodificador gera uma nova palavra na saída a cada etapa.

Mas como o decodificador sabe qual palavra deve ser gerada a cada vez? Porque lhe é passada a frase que já foi traduzida e, a cada etapa, ele gera a próxima palavra. Em outras palavras, a cada etapa, o decodificador recebe a frase que traduziu até o momento e gera a próxima palavra.

Mas, mesmo assim, como ele sabe que precisa gerar a primeira palavra? Porque lhe é passada uma palavra especial que significa "começar a traduzir" e, a partir daí, ele gera as palavras seguintes.

E, finalmente, como o transformador sabe que precisa parar de gerar palavras? Porque, quando termina de traduzir, ele gera uma palavra especial que significa "fim da tradução", que, quando volta para o transformador, significa que ele não gera mais palavras.

Agora que já entendemos isso em palavras, o que é mais simples, vamos colocar o detokenizador de volta na saída.

Transformador - codificador-decodificador] (https://pub-fb664c455eca46a2ba762a065ac900f7.r2.dev/Transformer-encoder-decoder.png)

Portanto, o decodificador gerará tokens. Para saber que precisa iniciar uma frase, é inserido um token especial comumente chamado de SOS (Start Of Sentence) e, para saber que precisa terminar, ele gera outro token especial comumente chamado de EOS (End Of Sentence).

E, assim como o codificador, o token de entrada precisa passar por uma camada de incorporação para converter os tokens em representações vetoriais.

Supondo que cada token seja equivalente a uma palavra, o processo de tradução seria o seguinte

No momento, temos esta arquitetura

Transformador - codificador-decodificador (detokenizador)](https://pub-fb664c455eca46a2ba762a065ac900f7.r2.dev/Transformer-encoder-decoder-detokenizer-2.webp)

Projeção

Dissemos que o decodificador recebe um token que passa pela camada de incorporação Output embedding.

O decodificador Output cria um vetor para cada token, de modo que na saída do decodificador Output temos uma matriz de ($n_{output-tokens}$ x $d_{model}$).

O decodificador executa operações, mas gera uma matriz com a mesma dimensão. Portanto, ele precisa converter essa matriz em um token, e faz isso por meio de uma camada linear que gera uma matriz com a mesma dimensão dos possíveis tokens no idioma a ser traduzido (vocabulário de saída).

Essa matriz corresponde aos logits de cada token possível e, portanto, é passada por uma camada softmax que converte esses logits em probabilidades. Ou seja, teremos a probabilidade de que cada token seja o próximo token.

Transformer - projeção](https://pub-fb664c455eca46a2ba762a065ac900f7.r2.dev/Transformer-projection.webp)

Codificador e decodificador x6

No documento original, eles usam 6 camadas para o codificador e outras 6 camadas para o decodificador. Não há motivo para que sejam 6. Acho que eles tentaram vários valores e esse foi o que funcionou melhor para eles.

A saída do último codificador é enviada para cada decodificador.

Transformador - codificador-decodificador (x6)](https://pub-fb664c455eca46a2ba762a065ac900f7.r2.dev/Transformer-encoder-decoder-x6.webp)

Para simplificar o diagrama, vamos representá-lo da seguinte forma

Transformador - codificador-decodificador (Nx)](https://pub-fb664c455eca46a2ba762a065ac900f7.r2.dev/Transformer-encoder-decoder-Nx.webp)

Atenção - Alimentação

Vamos começar a examinar o que há dentro do codificador e do decodificador. Basicamente, o que você tem é um mecanismo de atenção e uma camada de avanço.

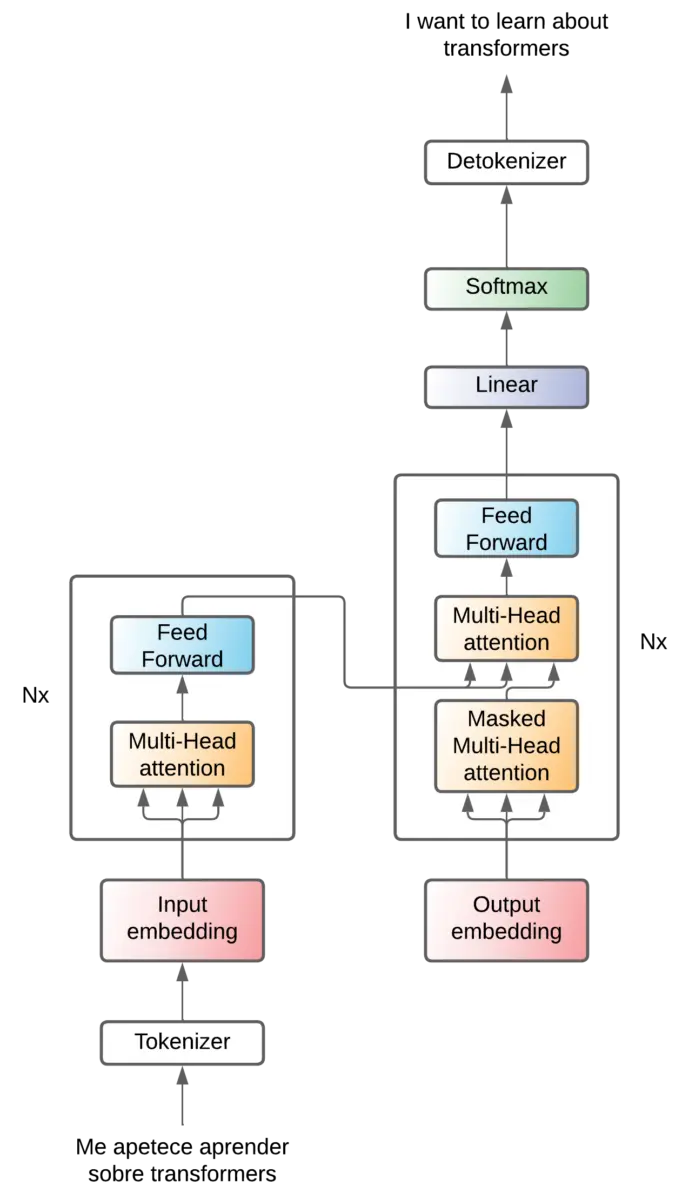
Atenção

Podemos ver que três setas entram nos mecanismos de atenção. Veremos isso mais tarde, quando analisarmos em profundidade como funcionam os mecanismos de atenção.

Mas, por enquanto, podemos dizer que são operações realizadas para obter a relação que existe entre os tokens (e, portanto, a relação que existe entre as palavras).

Antes dos transformadores, as redes neurais recorrentes eram usadas para o problema de tradução, que consistia em redes que recebiam um token de entrada, processavam-no e geravam outro token de saída. Em seguida, um segundo token era inserido, processado e outro token era gerado, e assim por diante com todos os tokens na sequência de entrada. O problema com essas redes é que, quando as frases eram muito longas, quando os últimos tokens eram inseridos, a rede "esquecia" os primeiros tokens. Por exemplo, em frases muito longas, poderia acontecer de o gênero do sujeito mudar ao longo da frase traduzida. E isso acontecia porque, depois de muitos tokens, a rede esquecia se o sujeito era masculino ou feminino.

Para resolver isso, a sequência inteira é inserida no mecanismo de atenção dos transformadores e as relações (atenção) entre todos os tokens são calculadas de uma só vez.

Isso é muito eficiente, pois em um único cálculo ele fornece a relação entre todos os tokens, independentemente do tamanho da sequência.

Embora essa seja uma grande vantagem e seja o que levou os transformadores a serem usados na maioria das melhores redes modernas, também é sua maior desvantagem, pois o cálculo da atenção é muito caro do ponto de vista computacional. Ele requer multiplicações de matrizes muito grandes.

Essas multiplicações são realizadas entre matrizes que correspondem às incorporações de cada um dos tokens por si só. Ou seja, a matriz que representa as incorporações dos tokens é multiplicada por ela mesma. Para realizar essa multiplicação, uma das matrizes deve ser girada (requisitos de álgebra para poder multiplicar matrizes). Assim, uma matriz é multiplicada por ela mesma; se a sequência de entrada tiver mais tokens, as matrizes que estão sendo multiplicadas serão maiores, uma em altura e outra em largura, de modo que a memória necessária para armazenar essas matrizes aumentará quadraticamente.

Portanto, à medida que o comprimento das sequências aumenta, a quantidade de memória necessária para armazenar essas matrizes cresce quadraticamente. E essa é uma grande limitação atual, a quantidade de memória que as GPUs têm, que é onde essas multiplicações geralmente são realizadas.

Uma única camada de atenção é usada no codificador para extrair as relações entre os tokens de entrada.

Duas camadas de atenção são usadas no decodificador, uma para extrair as relações entre os tokens de saída e outra para extrair as relações entre os tokens do codificador e os tokens do decodificador.

Alimentação

Após a camada de atenção, a sequência entra em uma camada de Feed forward que tem duas finalidades

• Uma delas é adicionar não linearidades. Como explicamos, a atenção é obtida por meio de multiplicações de matrizes dos tokens das sequências de entrada. Mas se nenhuma camada não linear for aplicada a uma rede, no final, toda a arquitetura poderá ser resumida em alguns cálculos lineares. Portanto, as redes neurais não seriam capazes de resolver problemas não lineares. Portanto, essa camada é adicionada para acrescentar a não linearidade.

• Outra é a extração de recursos. Embora a atenção já extraia recursos, esses são recursos das relações entre tokens. Mas essa camada Feed forward é responsável por extrair recursos dos próprios tokens. Ou seja, os recursos são extraídos de cada token que são considerados importantes para o problema que está sendo resolvido.

Codificação posicional

Explicamos que na camada de atenção são obtidas as relações entre os tokens, que essa relação é calculada por multiplicações de matrizes e que essas multiplicações são realizadas entre a matriz de incorporação por si só. Portanto, nas sentenças O gato come peixe e O peixe come gato, a relação entre o e gato é a mesma em ambas as sentenças, uma vez que a relação é calculada por meio de multiplicações de matrizes dos embeddings de o e gato.

Entretanto, na primeira, the se refere ao cat, enquanto na segunda the se refere ao fish. Portanto, além das relações entre as palavras, precisamos ter algum mecanismo para indicar sua posição na frase.

No documento, eles propõem a introdução de um mecanismo de atenção que é responsável por adicionar valores aos vetores de incorporação.

Transformador - codificação posicional](https://pub-fb664c455eca46a2ba762a065ac900f7.r2.dev/Transformer-positional-encoding.webp)

A fórmula para calcular esses valores é

Transformador - codificação posicional (fórmula)](https://pub-fb664c455eca46a2ba762a065ac900f7.r2.dev/Transformer-positional-encoding-formula.webp)

Como isso é um pouco difícil de entender, vamos ver como seria uma distribuição de valores da "codificação posicional".

Transformador - codificação posicional (diagrama)](https://pub-fb664c455eca46a2ba762a065ac900f7.r2.dev/Transformer-positional-encoding-diagram.webp)

O primeiro token terá os valores da primeira linha (a inferior) adicionados a ele, o segundo token terá os valores da segunda linha, e assim por diante, o que causa uma alteração nos embeddings, conforme mostrado na figura. Visto em duas dimensões, você pode ver as ondas que estão sendo adicionadas.

Essas ondas significam que, quando são feitos cálculos de atenção, as palavras mais próximas estão mais relacionadas do que as palavras mais distantes.

Mas podemos pensar em algo: se o processo de incorporação consiste em criar um espaço vetorial no qual palavras com o mesmo significado semântico estão próximas umas das outras, essa relação não seria quebrada se valores fossem adicionados às incorporações?

Se olharmos novamente para o exemplo do espaço vetorial anterior

Podemos ver que os valores variam mais ou menos de -1000 a 1000 em cada eixo, enquanto o gráfico de distribuições

Transformador - codificação posicional (diagrama)](https://pub-fb664c455eca46a2ba762a065ac900f7.r2.dev/Transformer-positional-encoding-diagram.webp)

variam de -1 a 1, pois esse é o intervalo das funções seno e cosseno.

Portanto, estamos variando em um intervalo entre -1 e 1 os valores dos embeddings, que são duas ou três ordens de magnitude a mais, de modo que a variação será muito pequena em comparação com o valor dos embeddings.

Portanto, já temos uma maneira de conhecer a relação da posição dos tokens na frase.

Add & Norm

Resta apenas um bloco de alto nível, que são as camadas Add & Norm.

Transformer - Add & norm](https://pub-fb664c455eca46a2ba762a065ac900f7.r2.dev/Transformer-Add-norm.webp)

Essas camadas são adicionadas após cada camada de atenção e camada de avanço. Essa camada agrega a saída e a entrada de uma camada. Isso é chamado de conexões residuais e tem as seguintes vantagens

• Durante o treinamento:

  • Reduzem o problema do desvanecimento do gradiente: Quando uma rede neural é muito grande, no processo de treinamento, os gradientes se tornam cada vez menores à medida que você se aprofunda nas camadas. Isso faz com que as camadas mais profundas não consigam atualizar bem seus pesos. As conexões residuais permitem que os gradientes passem diretamente pelas camadas, o que ajuda a mantê-los grandes o suficiente para que o modelo continue aprendendo, mesmo nas camadas mais profundas.

  • Permitir o treinamento de redes mais profundas: ao ajudar a atenuar o problema do desvanecimento do gradiente, as conexões residuais também facilitam o treinamento de redes mais profundas, o que pode levar a um melhor desempenho.

• Durante a inferência:

  • Permitem a transmissão de informações entre diferentes camadas: como as conexões residuais permitem que a saída de cada camada se torne a soma da entrada e da saída da camada, as informações das camadas mais profundas são transmitidas para as camadas de nível mais alto. Isso pode ser benéfico em muitas tarefas, especialmente quando as informações de baixo nível e de alto nível podem ser úteis.

  • Melhorar a robustez do modelo: como as conexões residuais permitem que as camadas aprendam melhor em camadas mais profundas, os modelos com conexões residuais podem ser mais robustos a perturbações nos dados de entrada.

  • Permitem a recuperação de informações perdidas: se algumas informações forem perdidas durante a transformação em qualquer camada, as conexões residuais podem permitir que essas informações sejam recuperadas nas camadas subsequentes.

Essa camada é chamada de Add & Norm, já vimos a Add, vamos dar uma olhada na Norm. A normalização é adicionada para que a adição da entrada e da saída não acione os valores.

Já vimos todas as camadas de alto nível do transformador.

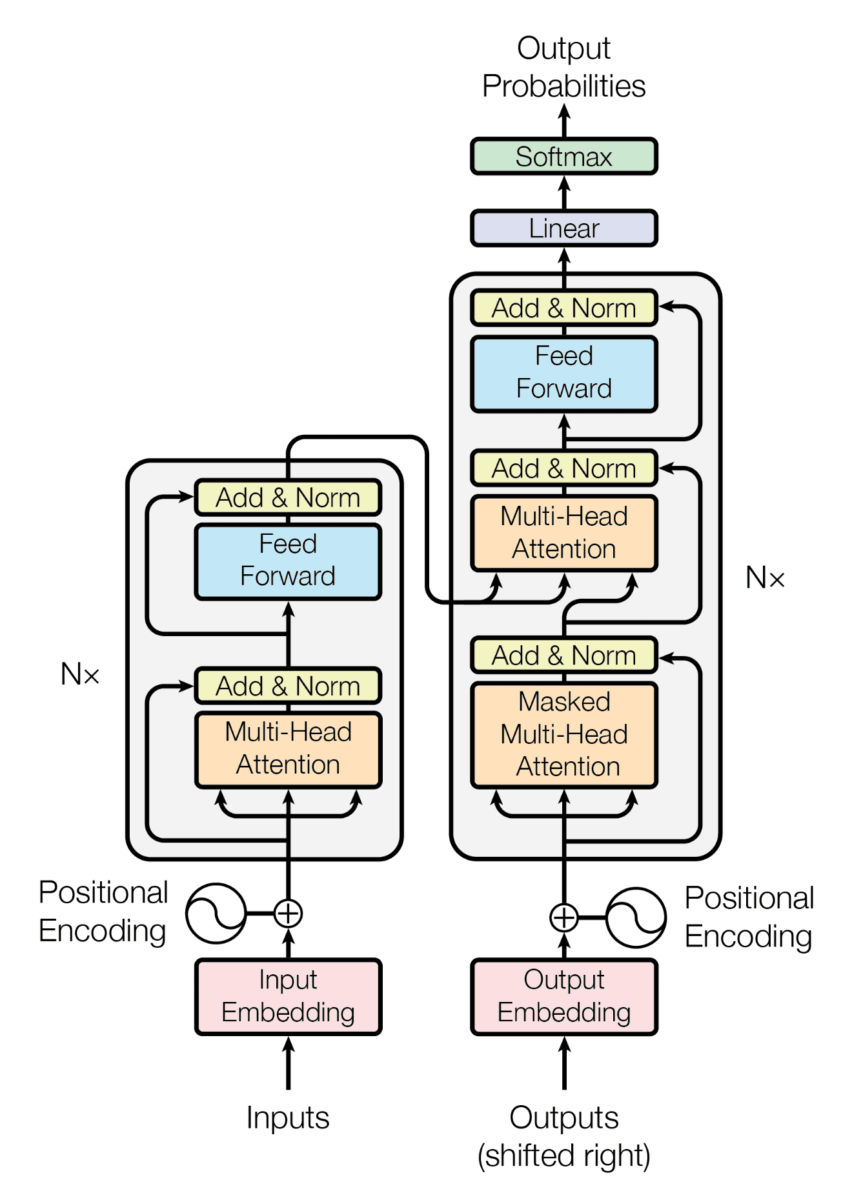
para que possamos examinar a parte mais importante que dá nome ao documento, os mecanismos de atenção.

Mecanismos de atendimento

Atenção a várias cabeças

Antes de analisarmos o mecanismo real da atenção, temos que analisar a atenção de várias cabeças.

Transformador - atenção a vários cabeçotes] (https://pub-fb664c455eca46a2ba762a065ac900f7.r2.dev/Transformer-multi-head-attention.webp)

Quando explicamos as camadas de alto nível, vimos que nas camadas de atenção havia 3 setas, que são Q, K e V. Essas são matrizes que correspondem às informações de tokens; no caso do mecanismo de atenção do codificador, elas correspondem aos tokens da sentença do idioma original e, no caso da camada de atenção do decodificador, elas correspondem aos tokens da sentença que foi traduzida até o momento e à saída do codificador.

Não nos importamos com a origem dos tokens agora, apenas lembre-se de que eles correspondem a tokens. Conforme explicado acima, os tokens são convertidos em embeddings, de modo que Q, K e V são matrizes de tamanho ($n_{tokens}$ x $d_{model}$). Normalmente, a dimensão de incorporação ($d_{model}$) é um número grande, como 512, 1024, 2048 etc. (não precisa ser uma potência de 2, esses são apenas exemplos).

Já explicamos que os embeddings são representações vetoriais de tokens. Ou seja, os tokens são convertidos em espaços vetoriais nos quais as palavras com significado semântico semelhante estão muito próximas.

Portanto, de todas essas dimensões, algumas podem estar relacionadas a características morfológicas, outras a características sintáticas, outras a características semânticas etc. Portanto, faz sentido calcular os mecanismos de atenção entre as dimensões de embeddings com características semelhantes.

Lembre-se de que os mecanismos de atenção buscam a similaridade entre as palavras, portanto, faz sentido buscar a similaridade entre recursos semelhantes.

Portanto, antes de calcular os mecanismos de atenção, as dimensões de incorporação são separadas em grupos de características semelhantes, e os mecanismos de atenção entre esses grupos são calculados.

E como essa separação é feita? Você teria que procurar dimensões semelhantes, mas fazer isso em um espaço de 512, 1024, 2048 etc. dimensões é muito complicado. Além disso, não é possível saber quais características são semelhantes e, em cada caso, as características consideradas semelhantes mudarão.

As projeções lineares são, portanto, usadas para separar as dimensões em grupos. Em outras palavras, os embeddings passam por camadas lineares que os separam em grupos de características semelhantes. Dessa forma, durante o treinamento do transformador, os pesos das camadas lineares serão alterados até chegar a um ponto em que o agrupamento seja feito de maneira ideal.

Agora podemos ter a questão de em quantos grupos devemos nos dividir. No documento original, ele é dividido em 8 grupos, mas não há motivo para que sejam 8. Acho que eles tentaram vários valores e esse foi o que funcionou melhor para eles.

Uma vez que as incorporações tenham sido divididas em grupos semelhantes e a atenção nos diferentes grupos tenha sido calculada, os resultados são concatenados. Isso é lógico, suponhamos que tenhamos um ebedding de 512 dimensões e o dividamos em 8 grupos de 64 dimensões. Se calcularmos a atenção em cada um dos grupos, teremos 8 matrizes de atenção de 64 dimensões; se as concatenarmos, teremos uma matriz de atenção de 512 dimensões, que é a mesma dimensão que tínhamos no início.

Mas a concatenação faz com que todos os recursos fiquem juntos. As primeiras 64 dimensões correspondem a um recurso, as 64 seguintes a outro, e assim por diante. Portanto, para misturá-los novamente, você passa por uma camada linear que mistura todos os recursos. E essa combinação é aprendida durante o treinamento.

Atenção ao produto de ponto de escala

Chegamos à parte mais importante do transformador, o mecanismo de atenção, a "atenção do produto escalonado de pontos".

Transformador - atenção ao produto de pontos em escala](https://pub-fb664c455eca46a2ba762a065ac900f7.r2.dev/Transformer-scaled-dot-product-attention.webp) Transformador - fórmula de atenção do produto escalonado](https://pub-fb664c455eca46a2ba762a065ac900f7.r2.dev/Transformer-scaled-dot-product-attention-formula.webp)

Como vimos, na arquitetura do Transformer há três mecanismos de atendimento

O codificador, o decodificador e o codificador-decodificador. Portanto, vamos explicá-los separadamente, pois, embora sejam praticamente os mesmos, eles têm algumas pequenas diferenças.

Atenção ao produto de pontos da escala Endocer

Vamos examinar novamente o diagrama de blocos e a fórmula.

Transformador - atenção ao produto de pontos em escala](https://pub-fb664c455eca46a2ba762a065ac900f7.r2.dev/Transformer-scaled-dot-product-attention.webp) Transformador - fórmula de atenção do produto escalonado](https://pub-fb664c455eca46a2ba762a065ac900f7.r2.dev/Transformer-scaled-dot-product-attention-formula.webp)

Primeiro, vamos entender por que havia três setas entrando nas camadas de atenção. Se observarmos a arquitetura do transformador, a entrada do codificador se divide em três e entra na camada de atenção.

Portanto, K, Q e V são o resultado da incorporação e da codificação posicional. A mesma matriz é colocada na camada de atenção três vezes. Devemos lembrar que essa matriz consistia em uma lista de todos os tokens ($n_{tokens}$), e cada token foi convertido em um vetor de embeddings de dimensão $d_{model}$, de modo que a dimensão da matriz será ($n_{tokens}$ x $d_{model}$).

O significado de K, Q e V vem dos bancos de dados key, query e value. O mecanismo de atenção recebe as matrizes Q e K, ou seja, a pergunta e a chave, e a saída é a matriz V, ou seja, a resposta.

Vamos analisar cada bloco separadamente para entender melhor isso.

Matmul

Esse bloco corresponde à multiplicação matricial das matrizes Q e K. Mas, para realizar essa operação, temos de fazê-la com a matriz transposta de K. Como as duas matrizes têm dimensão ($n_{tokens}$ x $d_{model}$), para multiplicá-las, a matriz K precisa ser transposta.

Portanto, teremos uma multiplicação de uma matriz de dimensão ($n_{tokens}$$ x $d_{model}$$) por outra matriz de dimensão ($d_{model}$$ x $n_{tokens}$), de modo que o resultado será uma matriz de dimensão ($n_{tokens}$$ x $n_{tokens}$).

Transformer - matmul](https://pub-fb664c455eca46a2ba762a065ac900f7.r2.dev/Transformer-matmul.webp)

Como podemos ver, o resultado é uma matriz em que a diagonal é a multiplicação da incorporação de cada token por ela mesma, e o restante das posições são as multiplicações entre as incorporações de cada token.

Agora vamos ver por que essa multiplicação é feita. Na postagem anterior [Measuring similarity between embeddings] (https://maximofn.com/embeddings-similarity/), vimos que uma maneira de obter a similaridade entre dois vetores de incorporação é calcular o cosseno

Na figura acima, é possível ver que a multiplicação entre as matrizes Q e K corresponde à multiplicação dos embeddings de cada token. A multiplicação entre dois vetores é realizada da seguinte forma

$.

Ou seja, temos a multiplicação das normas por seu cosseno. Se os vetores fossem unitários, ou seja, suas normas fossem 1, a multiplicação de dois vetores seria igual ao cosseno entre os dois vetores, que é uma das medidas de similaridade entre vetores.

Assim, como em cada posição da matriz resultante temos a multiplicação entre os vetores de incorporação de cada token, na realidade, cada posição da matriz representará a similaridade entre cada token.

Relembrando o que eram embeddings, os embeddings eram representações vetoriais de tokens em um espaço vetorial, em que os tokens com similaridade semântica estão próximos uns dos outros.

Assim, com essa multiplicação, obtivemos uma matriz de similaridade entre os tokens da frase

Os elementos diagonais têm similaridade máxima (verde), os elementos de canto têm similaridade mínima (vermelho) e o restante dos elementos tem similaridade intermediária.

Scale

Vejamos novamente o diagrama de atenção do produto escalar de pontos e sua fórmula

Transformador - atenção ao produto de pontos em escala](https://pub-fb664c455eca46a2ba762a065ac900f7.r2.dev/Transformer-scaled-dot-product-attention.webp) Transformador - fórmula de atenção do produto escalonado](https://pub-fb664c455eca46a2ba762a065ac900f7.r2.dev/Transformer-scaled-dot-product-attention-formula.webp)

Dissemos que se, ao multiplicar Q por K, fizéssemos a multiplicação entre os vetores de incorporação e que, se esses vetores tivessem norma 1, o resultado seria a similaridade entre os vetores. Mas como os vetores não têm norma 1, o resultado pode ter valores muito altos, então normalizamos dividindo pela raiz quadrada da dimensão dos vetores de incorporação.

Mask (opcional)

O mascaramento é opcional e não é usado no codificador, portanto, não o explicaremos no momento para não confundir o leitor.

Transformador - atenção ao produto de pontos em escala](https://pub-fb664c455eca46a2ba762a065ac900f7.r2.dev/Transformer-scaled-dot-product-attention.webp) Transformador - fórmula de atenção do produto escalonado](https://pub-fb664c455eca46a2ba762a065ac900f7.r2.dev/Transformer-scaled-dot-product-attention-formula.webp)

Softmax

Embora tenhamos dividido pela raiz quadrada da dimensão dos vetores de incorporação, poderíamos fazer com que a similaridade entre os vetores de incorporação ficasse entre os valores 0 e 1, portanto, para garantir isso, passamos por uma camada softmax.

Transformador - atenção ao produto de pontos em escala](https://pub-fb664c455eca46a2ba762a065ac900f7.r2.dev/Transformer-scaled-dot-product-attention.webp) Transformador - fórmula de atenção do produto escalonado](https://pub-fb664c455eca46a2ba762a065ac900f7.r2.dev/Transformer-scaled-dot-product-attention-formula.webp)

Matmul

Agora que temos uma matriz de similaridade entre os vetores de incorporação, vamos multiplicá-la pela matriz V, que representa as incorporações dos tokens.

Transformador - matmul2](https://pub-fb664c455eca46a2ba762a065ac900f7.r2.dev/Transformer-matmul2.webp)

A multiplicação nos dá

Transformer - matmul2 result](https://pub-fb664c455eca46a2ba762a065ac900f7.r2.dev/Transformer-matmul2-result.webp)

Obtemos uma matriz com uma mistura de incorporações com sua similaridade. Em cada linha, obtemos uma mistura das incorporações, em que cada elemento da incorporação é ponderado de acordo com a similaridade do token nessa linha com o restante dos tokens.

Além disso, temos novamente uma matriz de tamanho ($n_{tokens}$ x $d_{model}$), que é a mesma dimensão que tínhamos no início.

Resumo

Em resumo, podemos dizer que a atenção ao produto de ponto escalonado é um mecanismo que calcula a similaridade entre os tokens de uma frase e, a partir dessa similaridade, calcula uma matriz de saída que corresponde a uma mistura de embeddings ponderados de acordo com a similaridade dos tokens.

Decodificador de escala mascarada atenção ao produto de pontos

Vamos examinar novamente a arquitetura do transformador.

Como podemos ver, nesse caso, a "atenção ao produto escalonado de pontos" tem a palavra "mascarado". Primeiro, explicaremos por que esse mascaramento é necessário e, em seguida, veremos como ele é feito.

Por que a máscara

Como dissemos, o transformador foi inicialmente concebido como um tradutor, mas, em geral, é uma arquitetura na qual você coloca uma sequência e ela produz outra sequência. No entanto, quando se trata de treinamento, é necessário fornecer a sequência de entrada e a sequência de saída e, a partir daí, o transformador aprende a traduzir.

Por outro lado, dissemos que o transformador gera um novo token a cada vez. Ou seja, ele recebe a sequência de entrada no codificador e um token de início de sequência especial no decodificador e, a partir daí, gera o primeiro token da sequência de saída.

Em seguida, a sequência de entrada é colocada de volta no codificador e o token gerado anteriormente no decodificador e, a partir daí, ele gera o segundo token da sequência de saída.

Em seguida, a sequência de entrada é colocada de volta no codificador e os dois tokens gerados anteriormente no decodificador e, a partir daí, ele gera o terceiro token da sequência de saída.

E assim por diante, até gerar um token especial de fim de sequência.

Mas no treinamento, como a sequência de entrada e saída é fornecida a ele de uma só vez, precisamos mascarar os tokens que ele ainda não gerou para que não possa vê-los.

Mask

Vamos examinar novamente o diagrama de blocos e a fórmula.

Transformador - atenção ao produto de pontos em escala](https://pub-fb664c455eca46a2ba762a065ac900f7.r2.dev/Transformer-scaled-dot-product-attention.webp) Transformador - fórmula de atenção do produto escalonado](https://pub-fb664c455eca46a2ba762a065ac900f7.r2.dev/Transformer-scaled-dot-product-attention-formula.webp)

O mascaramento é feito após o Scale e antes do Softmax. Como precisamos mascarar os tokens "futuros", o que pode ser feito é multiplicar a matriz Scale resultante por uma matriz que tenha 0 nas posições que queremos mascarar e 1 nas posições que não queremos mascarar.

Transformador - Máscara] (https://pub-fb664c455eca46a2ba762a065ac900f7.r2.dev/Transformer-Mask.webp)

Ao fazer isso, obtemos a mesma matriz de antes, mas com posições mascaradas.

Transformer - Mask resutl](https://pub-fb664c455eca46a2ba762a065ac900f7.r2.dev/Transformer-Mask-resutl.webp)

Agora, o resultado do Scaled dot product attention é uma matriz com os embeddings dos tokens ponderados de acordo com a similaridade dos tokens, mas com os tokens que não devem ser mascarados.

Atenção ao produto de ponto da escala do codificador-decodificador

Vamos examinar novamente a arquitetura do transformador.

Agora vemos que o mecanismo de atenção recebe duas vezes a saída do codificador e uma vez a atenção mascarada do decodificador. Portanto, "K" e "V" são a saída do codificador e "Q" é a saída do decodificador.

Transformador - atenção ao produto de pontos em escala](https://pub-fb664c455eca46a2ba762a065ac900f7.r2.dev/Transformer-scaled-dot-product-attention.webp) Transformador - fórmula de atenção do produto escalonado](https://pub-fb664c455eca46a2ba762a065ac900f7.r2.dev/Transformer-scaled-dot-product-attention-formula.webp)

Portanto, nesse bloco de atenção, primeiro é calculada a similaridade entre a sentença do decodificador e a sentença do codificador, ou seja, é calculada a similaridade entre a sentença que foi traduzida até o momento e a sentença original.

Essa semelhança é então multiplicada pela sentença do codificador, ou seja, é obtida uma mistura de embeddings da sentença original, ponderada de acordo com a semelhança da sentença traduzida até o momento.

Resumo

Percorremos o transformador do nível mais alto ao mais baixo, para que você já tenha uma noção de como ele funciona.

Transformador - atenção a vários cabeçotes] (https://pub-fb664c455eca46a2ba762a065ac900f7.r2.dev/Transformer-multi-head-attention.webp) Transformador - atenção ao produto de pontos em escala](https://pub-fb664c455eca46a2ba762a065ac900f7.r2.dev/Transformer-scaled-dot-product-attention.webp)