Transformers - from top to the bottom

En este post vamos a ver cómo funcionan los Transformers de arriba a abajo.

Transformer como una caja negra

La arquitectura transformer se creo para el problema de traducción, por lo que vamos a explicarlo para ese problema

Imaginemos el transformer como una caja negra, a la que le entra una frase en un idioma y saca la misma frase traducida en otro idioma.

Tokenización

Pero como hemos visto en el post de tokens, los modelos de lenguaje no entienden las palabras como nosotros, sino que necesitan números para poder realizar las operaciones. Por lo que la frase en el idioma original se tiene que convertir a tokens mediante un tokenizador, y a la salida necesitamos un detokenizador para convertir los tokens de salida a palabras

De modo que el tokenizador crea una secuencia de $n_{input-tokens}$ tokens, y el detokenizador recibe una secuencia de $n_{output-tokens}$ tokens.

Input embeddings

En el post de embeddings vimos que los embeddings son una forma de representar las palabras en un espacio vectorial. Por lo que los tokens de entrada se pasan por una capa de embeddings para convertirlos en vectores.

En un resumen rápido, el proceso de embedding consiste en convertir una secuencia de números (tokens) en una secuencia de vectores. De manera que se crea un nuevo espacio vectorial en el que las palabras que tengan similitud semántia estarán cerca.

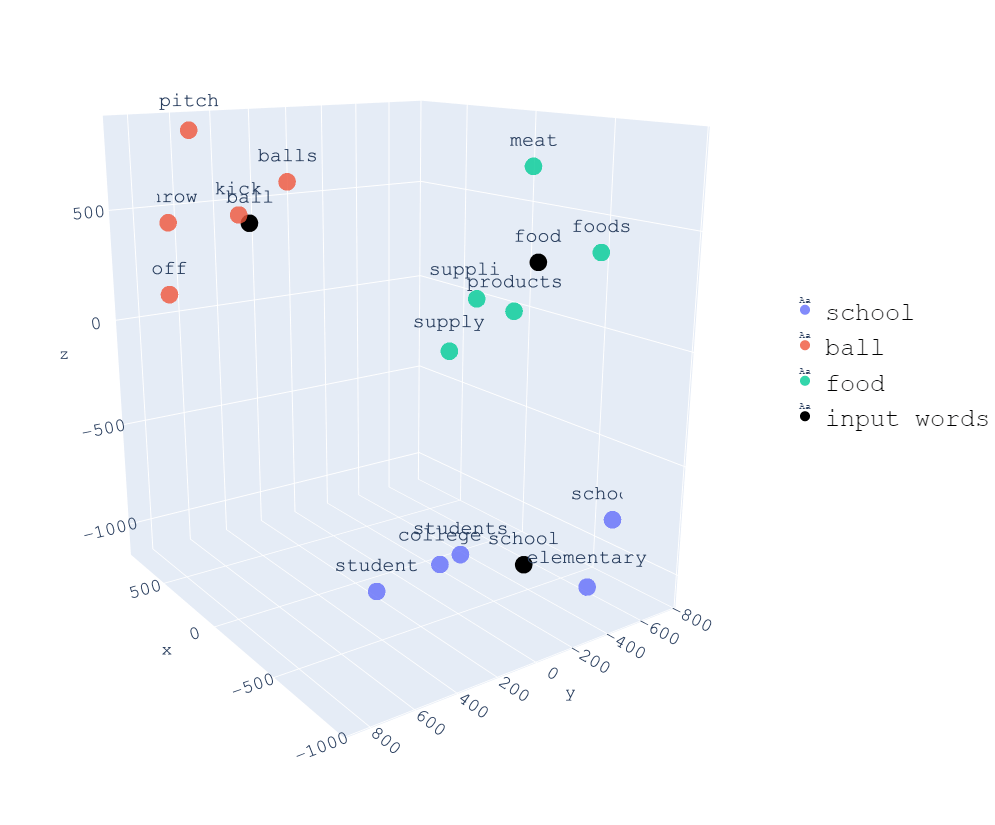
Si teníamos $n_{input-tokens}$ tokens, ahora tenemos $n_{input-tokens}$ vectores. Cada uno de esos vectores tiene una longitud de $d_{model}$. Es decir, cada token se convierte a un vector que representa ese token en un espacio vectorial de $d_{model}$ dimensiones. Por tanto después de pasar por la capa de embeddings, la secuencia de $n_{input-tokens}$ tokens se convierte en una matriz de ($n_{input-tokens}$ x $d_{model}$).

Encoder - decoder

Hemos visto el transformer actuando como una caja negra, pero en realidad el transformer es una arquitectura que se compone de dos partes, un encoder y un decoder.

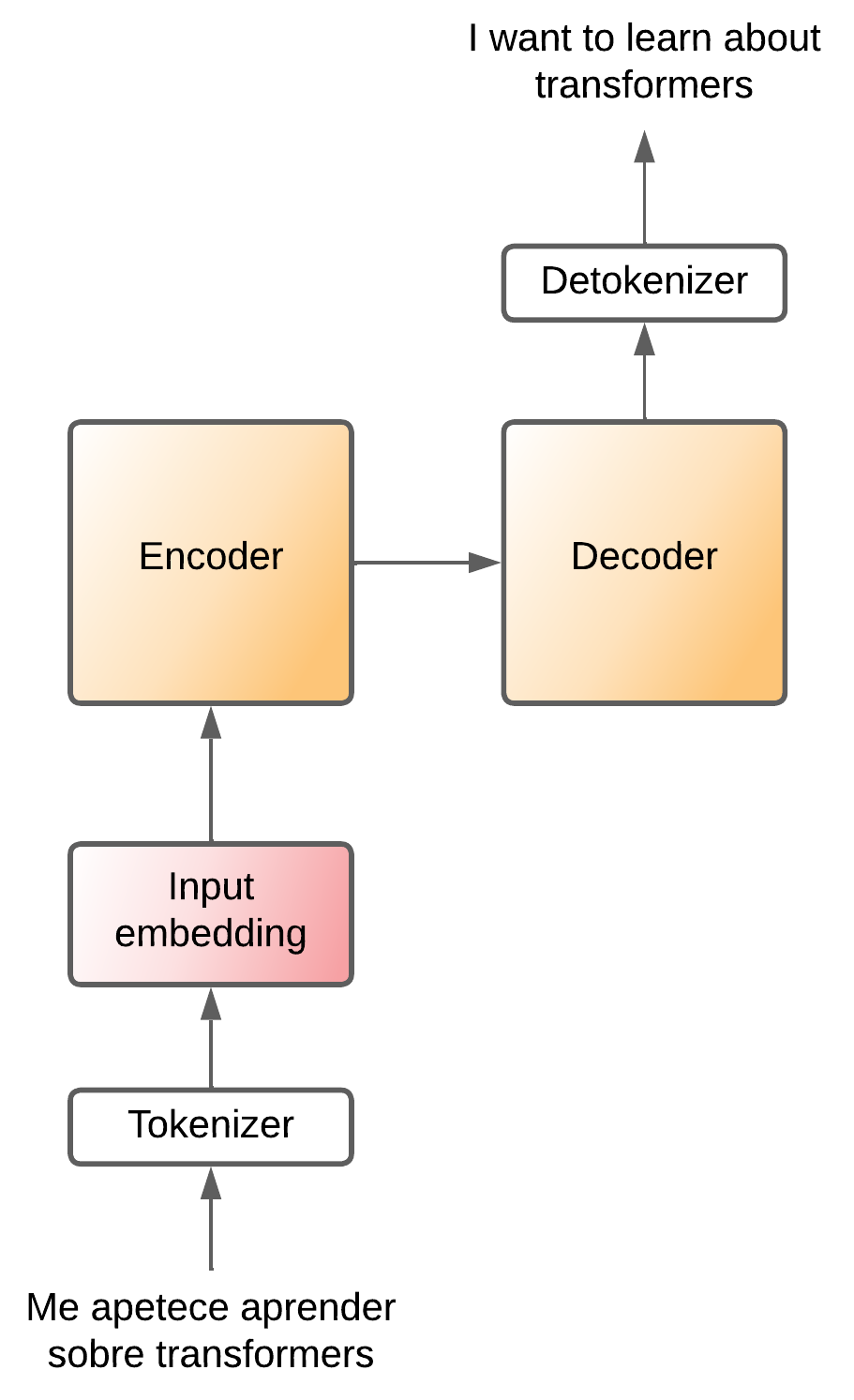
El encoder se encarga de comprimir la información de la frase de entrada, crea un espacio latente donde está esa información de la frase de entrada es comprimida. A continuación, esa información comprimida entra al decoder, que sabe convertir esa información comprimida en una frase del idioma de salida.

Y ¿cómo convierte el decoder esa información comprimida en una frase del idioma de salida? Pues token a token. Para entenderlo mejor vamos a olvidarnos de los tokens de salida por un momento, vamos a imaginar que tenemos esta arquitectura

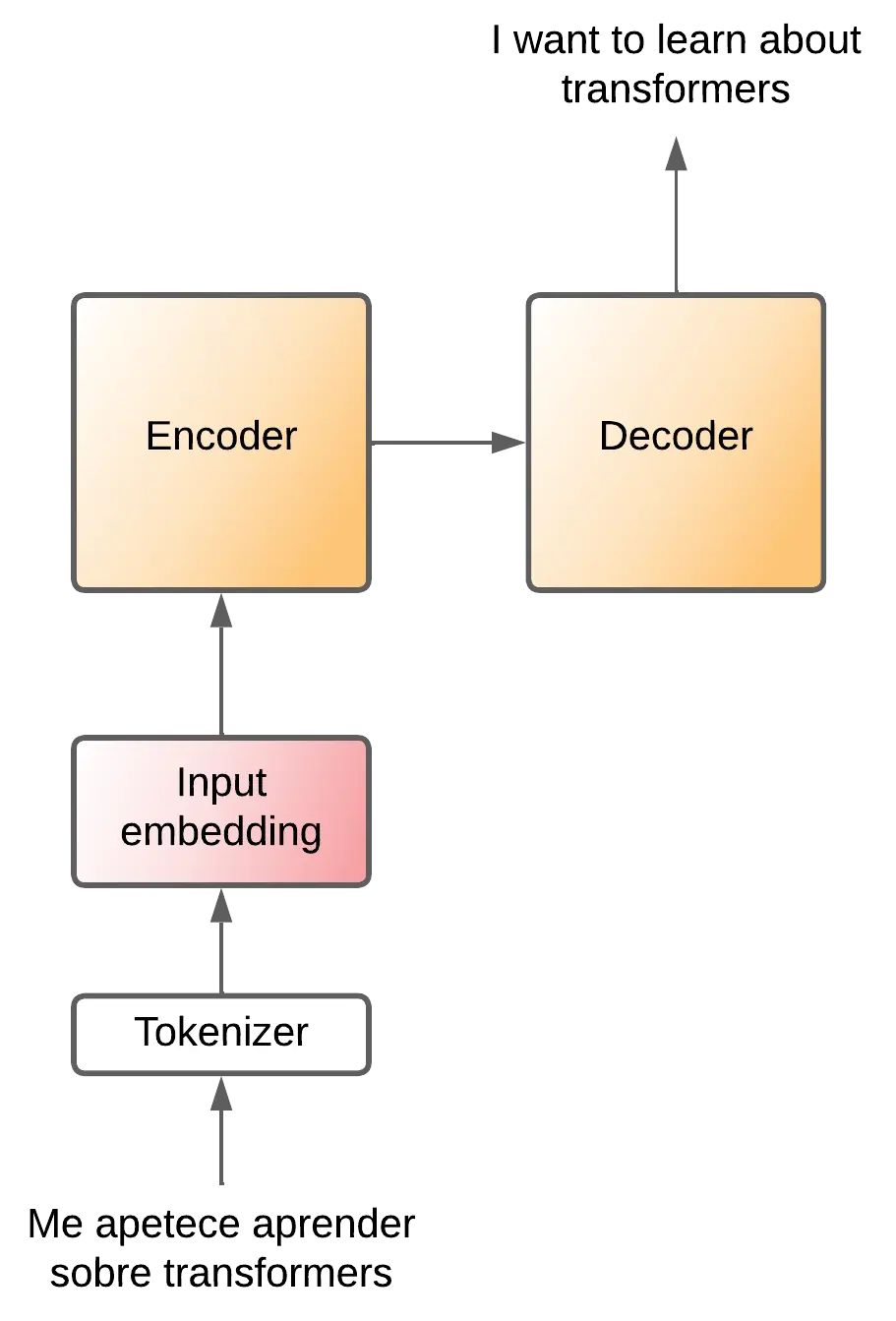
Es decir, la frase del idioma original se convierte a tokens, estos tokens se convierten a embeddings, que entran al encoder, este comprime la información, el decoder la coge y la convierte en palabras del idioma de salida

De modo que el decoder va generando una palabra nueva a la salida en cada paso

Pero ¿cómo sabe el decoder cúal es la palabra que tiene que generar cada vez? Porque se le está pasando la frase que ya ha traducido, y en cada paso va generando la siguiente palabra. Es decir, en cada paso el decoder recibe la frase que ha traducido hasta el momento, y genera la siguiente palabra.

Pero aun así, ¿cómo sabe que tiene que generar la primera palabra? Porque se le pasa una palabra especial que significa "empezar a traducir", y a partir de ahí va generando las siguientes palabras.

Y por último, ¿cómo sabe el transformer que tiene que dejar de generar palabras? Porque cuando termina de traducir genera una palabra especial que significa "fin de la traducción", que cuando vuelve a entrar al transformer hace que no genere más palabras.

Ahora que lo hemos entendido con palabras, que es más sencillo, vamos a volver a colocar el detokenizador a la salida

Por tanto el decoder irá generando tokens. Para saber que tiene que empezar una frase se le mete un token especial comunmente llamado SOS (Start Of Sentence), y para saber que tiene que terminar genera otro token especial comunmente llamado EOS (End Of Sentence).

Y al igual que el encoder, el token de entrada tiene que pasar por una capa de embedding para convertir los tokens en representaciones vectoriales.

Suponiendo que cada token equivale a una palabra, el proceso de traducción sería el siguiente

De momento tenemos esta arquitectura

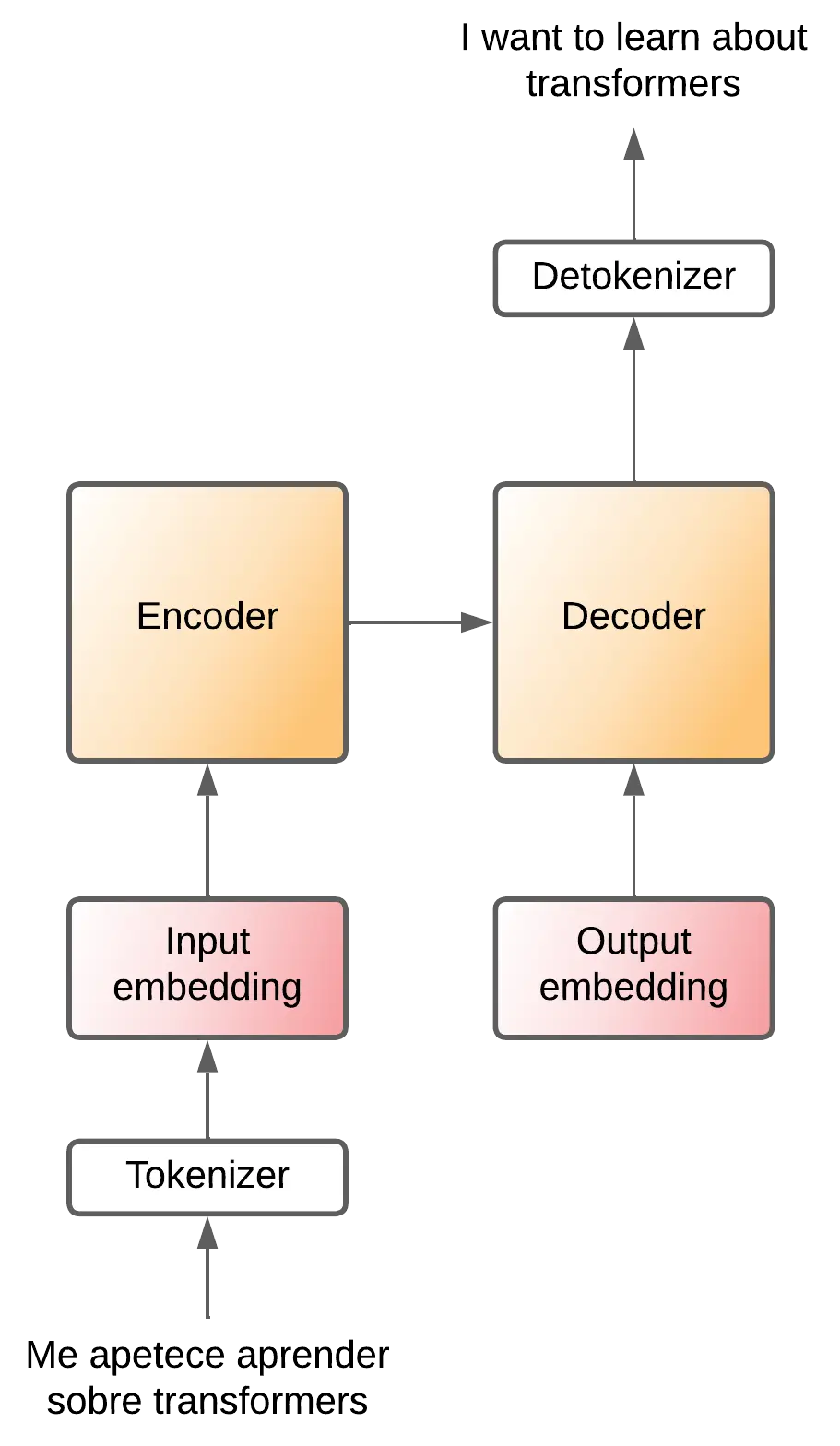
Projection

Hemos dicho que al decoder le entra un token que pasa por la capa de embedding Output embedding.

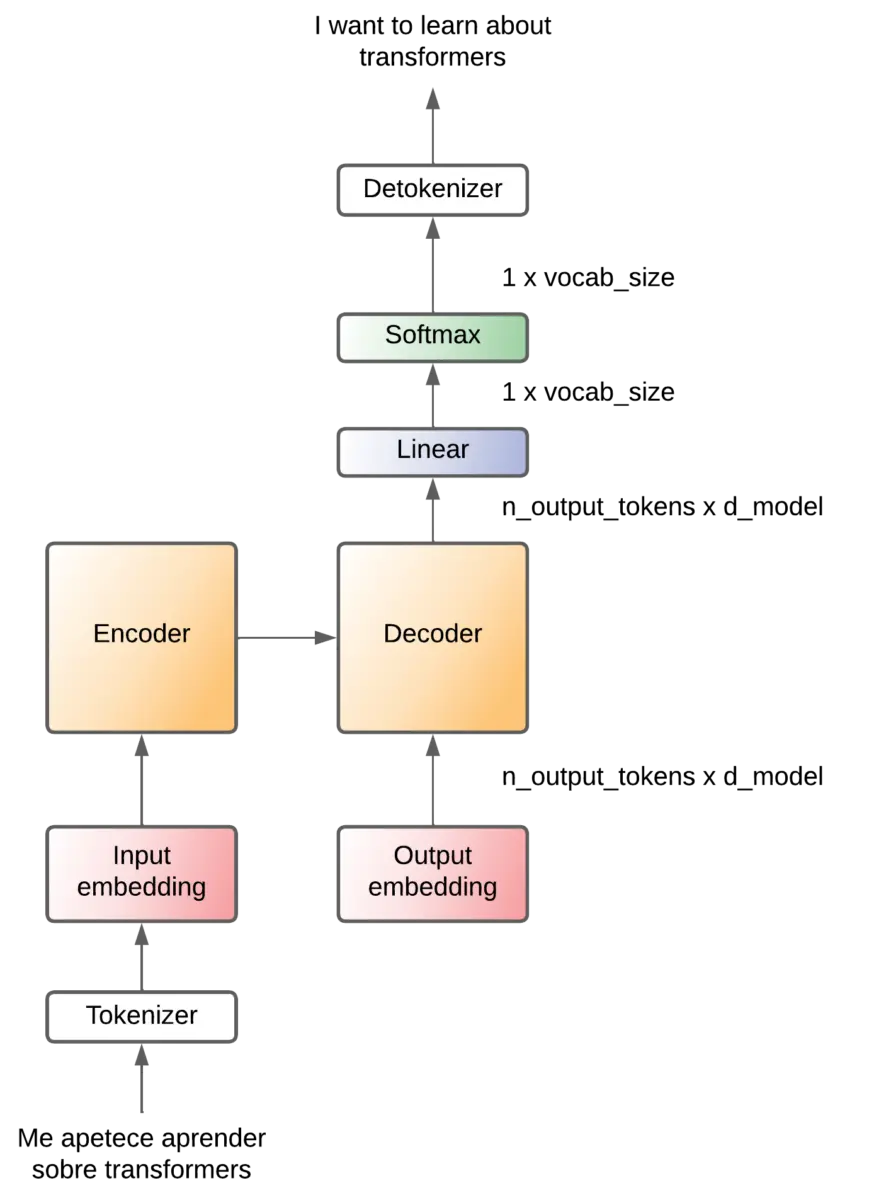
El Output decoder crea un vector por cada token, por lo que a la salida del Output decoder tenemos una matriz de ($n_{output-tokens}$ x $d_{model}$).

El decoder hace operaciones, pero saca una matriz con la misma dimensión. Así de necesita convertir esa matriz en un token y eso lo hace mediante una capa lineal que a la salida genera un array con la misma dimensión que los posibles tokens que hay en el lenguaje al que se quiere traducir (vocabulario de salida).

Ese array corresponde a los logits de cada posible token, por lo que a continuación se pasa por una capa softmax que convierte esos logits en probabilidades. Es decir, tendremos la probabilidad de que cada token sea el siguiente token.

Encoder y decoder x6

En el paper original usan 6 capas para el encoder y otras 6 capas para el decoder. No hay ninguna razón para que sean 6, supongo que probaron varios valores y este fue el que mejor les funcionó.

A cada uno de los decoder le entra la salida del último encoder

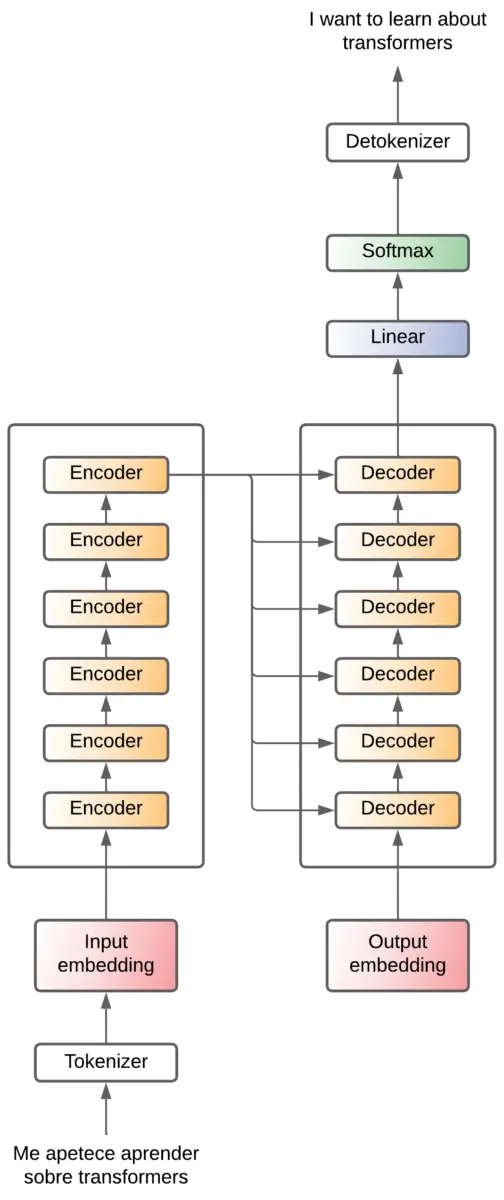
Para simplificar el diagrama lo representaremos así a partir de ahora

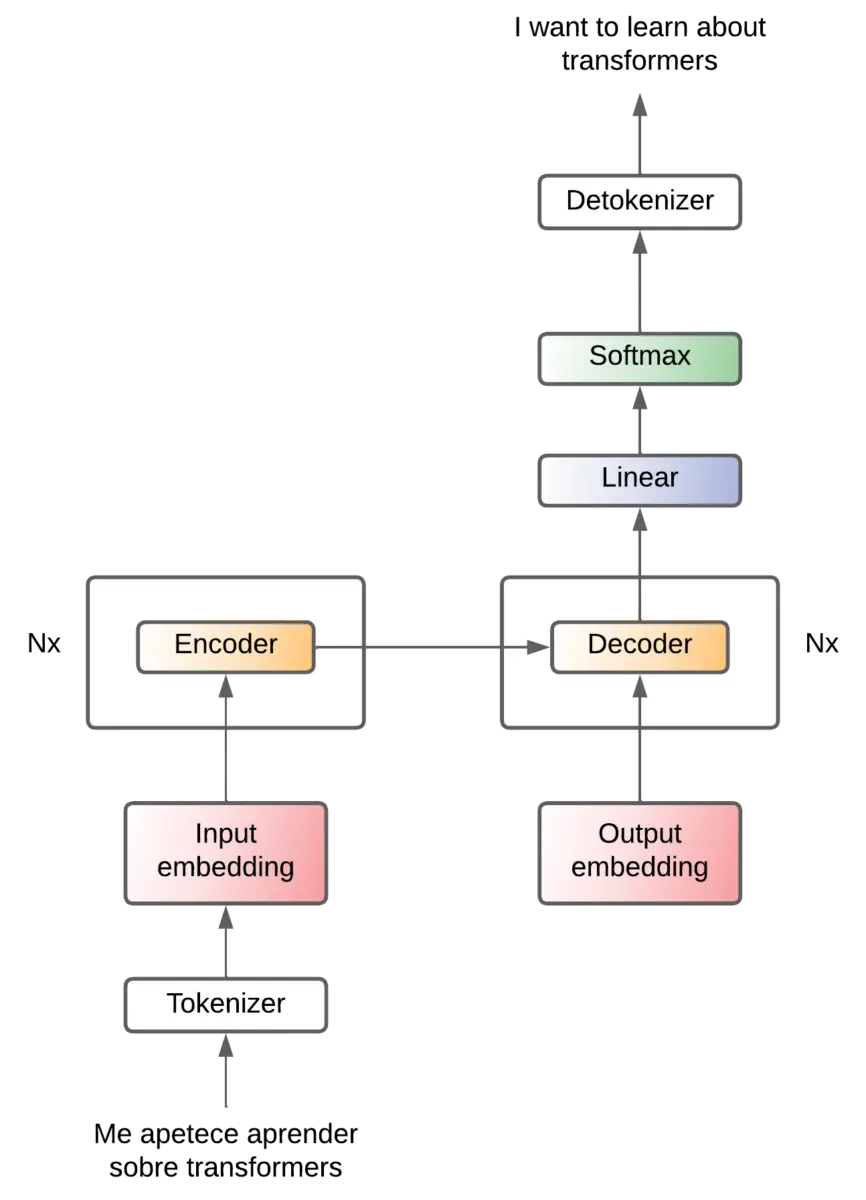
Attention - Feed forward

Vamos a ir empezando a ver qué ha dentro del encoder y el decoder. Básicamente lo que hay es un mecanismo de atención y una capa feed forward.

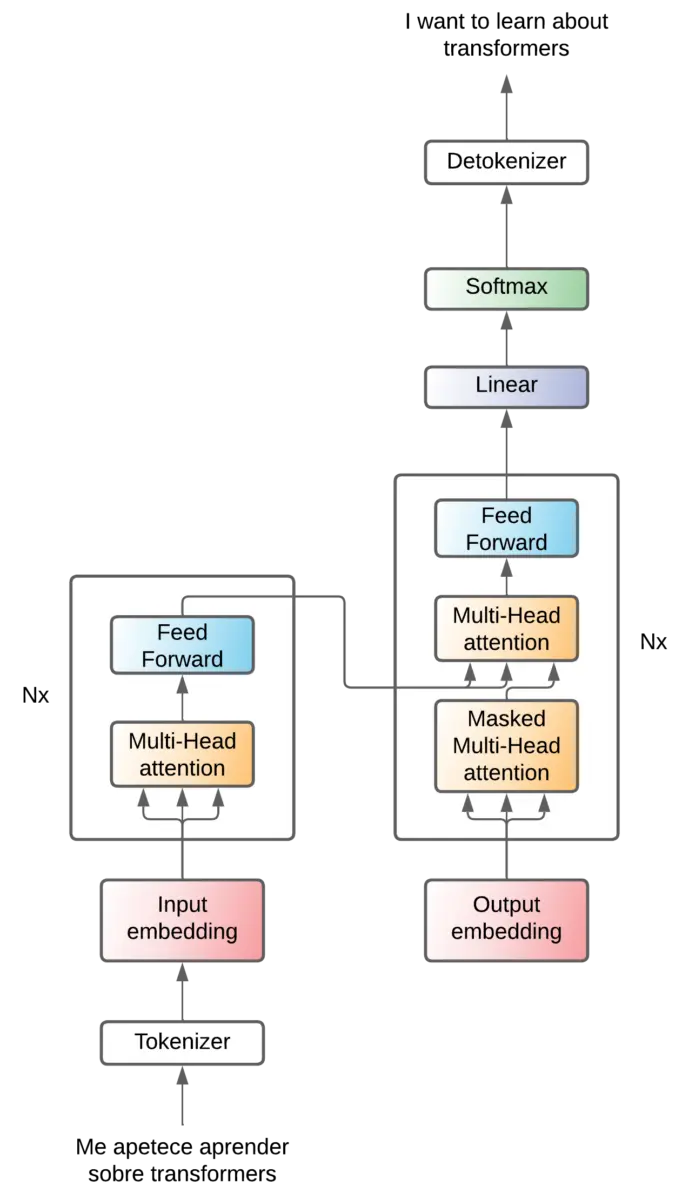
Atención

Podemos ver que en los mecanismos de atención entran 3 flechas. Esto ya lo veremos más adelante cuando veamos en profundidad cómo funcionan los mecanismos de atención.

Pero de momento podemos decir que son operaciones que se realizan para poder obtener la relación que existe entre los tokens (y por tanto, la relación que existe entre las palabras).

Antes de los transformers, para el problema de traducción se usaban las redes neuronales recurrentes, que consistían en redes a las que les entraba un token, lo procesaban y generaban otro token de salida. A continuación le entraba un segundo token, lo procesaban y sacaban otro token, y así sucesivamente con todos los tokens de la secuencia de entrada. El problema de estas redes es que cuando las frases eran muy largas, cuando se estaba en los últimos tokens, la red se "olvidaba" de los primeros tokens. Por ejemplo en frases muy largas, podría pasar que se cambiase el género del sujeto a lo largo de la frase traducida. Y esto es porque después de muchos tokens, la red se había olvidado si el sujeto era masculino o femenino.

Para solucionar esto, en el mecanismo de atención de los transformers entra la secuencia entera y de una sola vez se calculan las relaciones (atención) entre todos los tokens.

Esto es muy potente, ya que en un solo cálculo se obtiene la relación entre todos los tokens, sea lo larga que sea la secuencia.

Aunque esto es una gran ventaja y es lo que ha hecho que los transformers ahora se utilicen en la mayoría de las mejores redes modernas, también es su mayor desventaja, ya que el cálculo de la atención es muy costoso computacionalmente. Ya que requiere unas multiplicaciones matriciales muy grandes.

Esas multiplicaciones se realizan entre matrices que corresponden a los embeddings de cada uno de los tokens por ellas mismas. Es decir, la matriz que representa los embeddings de los tokens se multiplica por ella misma. Para poder realizar esta multiplicación hay que rotar una de las matrices (requisitos del algebra para poder multiplicar matrices). Así que se multiplica una matriz por ella misma, si la secuencia de entrada tiene más tokens, las matrices que se multiplican son más grandes, una en alto y otra en ancho, por lo que la memoria necesaria para almacenar esas matrices crece de forma cuadrática.

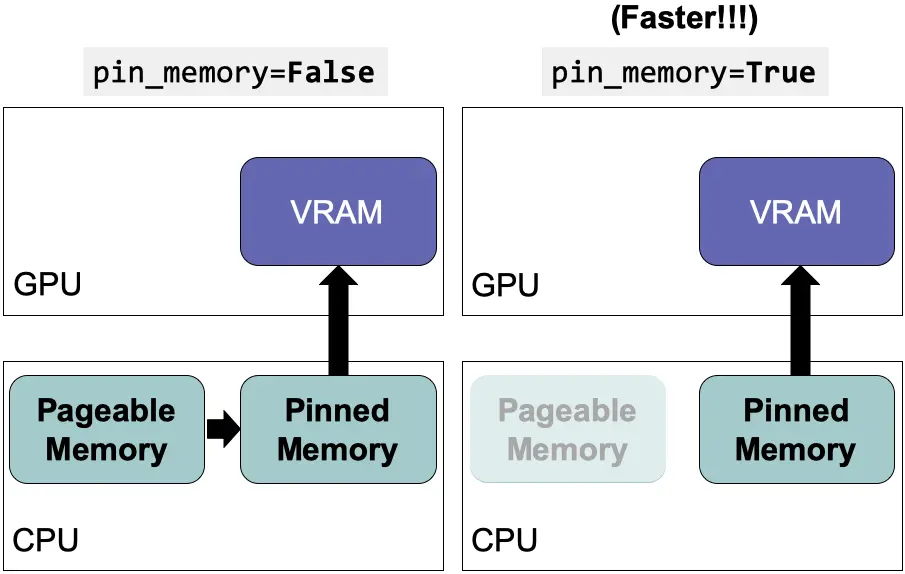
Por lo que a medida que aumenta la longitud de las secuencias, la cantidad de memoria necesaria para almacenar esas matrices crece de forma cuadrática. Y esto es un gran limitante a día de hoy, la cantidad de memoria que tienen las GPUs, que es dónde se suelen realizar esas multiplicaciones.

En el encoder se usa una sola capa de atención, para sacar las relaciones entre los tokens de entrada

En el decoder se utilizan dos capas de atención, una para sacar las relaciones entre los tokens de salida, y otra para sacar las relaciones entre los tokens del encoder y los del decoder.

Feed forward

Después de la capa de atención, la secuencia entra en una capa Feed forward que tiene dos propósitos

• Uno es añadir no linealidades. Como hemos explicado, la atención se consigue mediante multiplicaciones matriciales de los tokens de las secuencias de entrada. Pero si a una red no se le aplican capas no lineales, al final, toda la arquitectura se podría resumir en unos pocos cálculos lineales. Por lo que las redes neuronales no podrían resolveer problemas no lineales. De modo que se añade esta capa para añadir no linealidad

• Otro es extracción de características. Aunque la atención ya extrae características, estas son características de las relaciones entre los tokens. Pero esta capa Feed forward se encarga de extraer características de los tokens en sí. Es decir, de cada token se extraen características que se consideran importantes para el problema que se está resolviendo.

Positonal encoding

Hemos explicado que en la capa de atención se obtienen las relaciones entre los tokens, que esa relación se calcula mediante multiplicaciones matriciales y que esas multiplicaciones se realizan entre la matriz de embeddings por ella misma. Por lo que en las frases El gato come pescado y El pescado come gato, la relación entre el y gato es la misma en ambas frases, ya que la relación se calcula mediante multiplicaciones matriciales de los embeddings de el y gato.

Sin embargo, en la primera el se refiere a el gato, mientras que en la segunda el se refiere a el pescado. Por lo que además de las relaciones entre las palabras necesitamos tener algún mecanismo que nos indique su posición en la frase.

En el paper proponen meter un mecanismo de atención que se encarga de sumar unos valores a los vectores de embeddings

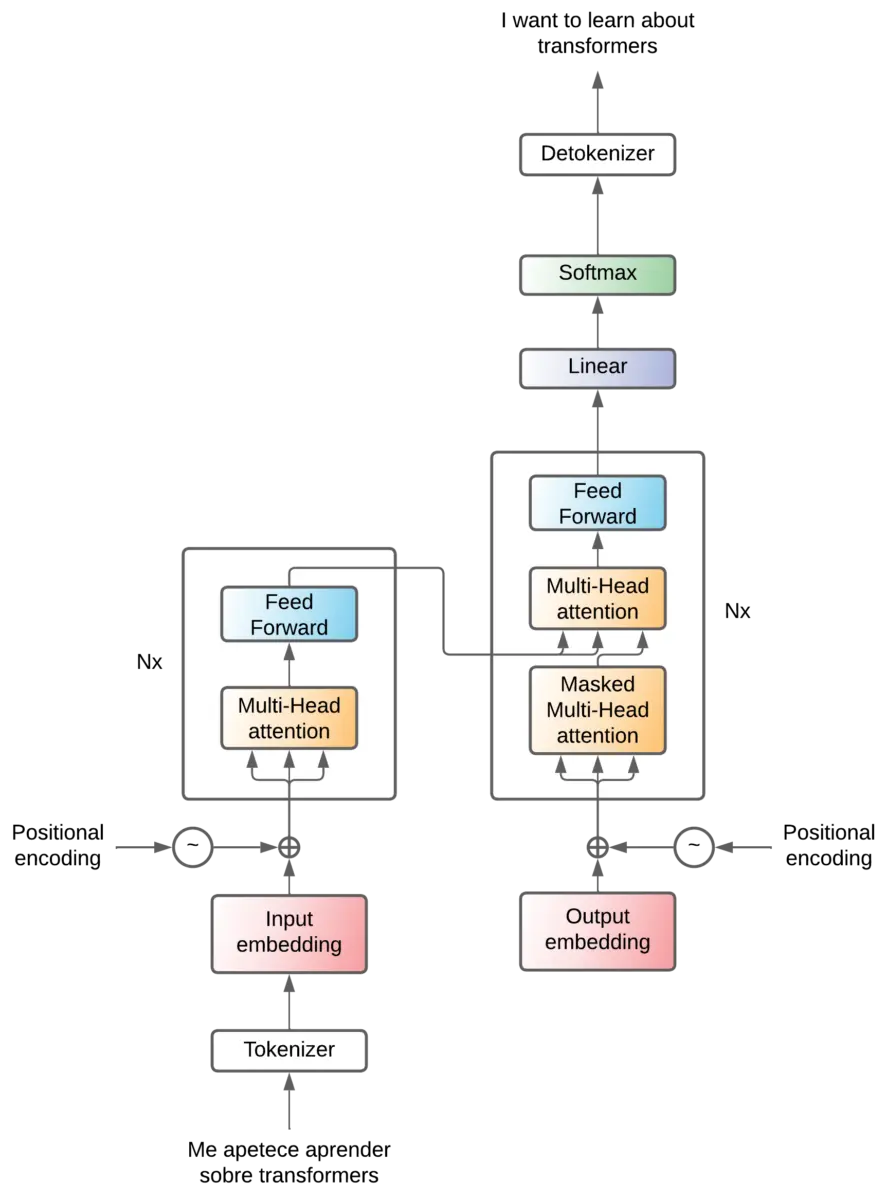
Donde la fórmula para calcular esos valores es

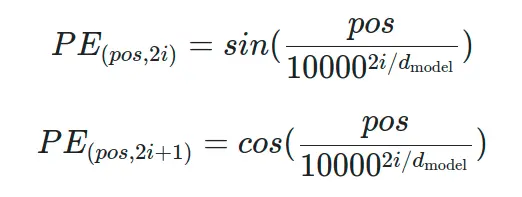
Como esto así en frío es un poco difícil de entender, vamos a ver cómo sería una distribución de valores del positional encoding

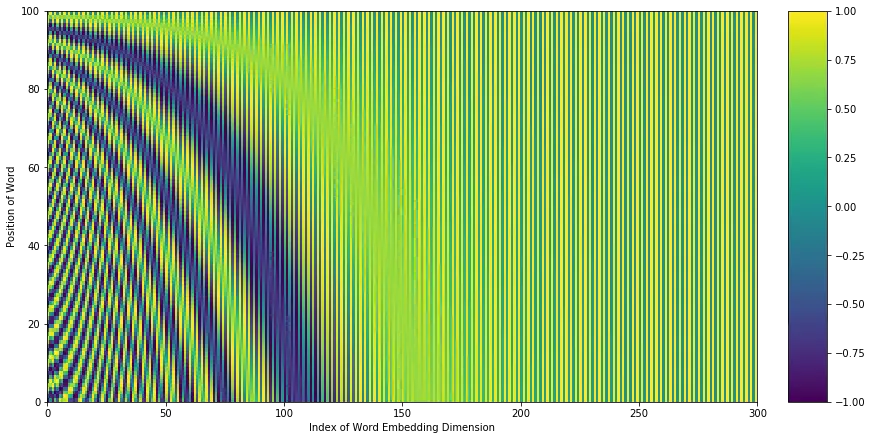
Al primer token se le van a sumar los valores de la primera fila (la de más abajo), al segundo token los de la segunda fila, y así sucesivamente, lo que provocan un cambio en los embeddings como se ve en la figura. Visto en dos dimensiones se aprecian las ondas que se van sumando.

Estas ondas hacen que cuando se realizan los cálculos de atención, las palabras más cercanas tengan más relación que las palabras más lejanas.

Pero podemos pensar una cosa, si el proceso de embedding consiste en crear un espacio vectorial en el que las palabras con el mismo significado semántico estén cerca, ¿no se estaría rompiendo esa relación si se suman valores a los embeddings?

Si nos volvemos a fijar en el ejemplo de espacio vectorial de antes

Podemos ver que los valores van más o menos de -1000 a 1000 en cada eje, mientras que la gráfica de distribuciones

los valores van de -1 a 1, ya que es el rango de las funciones seno y coseno.

Por lo que estamos variando en un rango de entre -1 y 1 los valores de los embeddings que tienen dos o tres órdenes de magnitud más, por lo que la variación va a ser muy pequeña en comparación con el valor de los embeddings.

De modo que ya tenemos una manera de saber la relación de la posición de los tokens en la frase

Add & Norm

Solo nos queda un bloque de alto nivel y son las capas Add & Norm

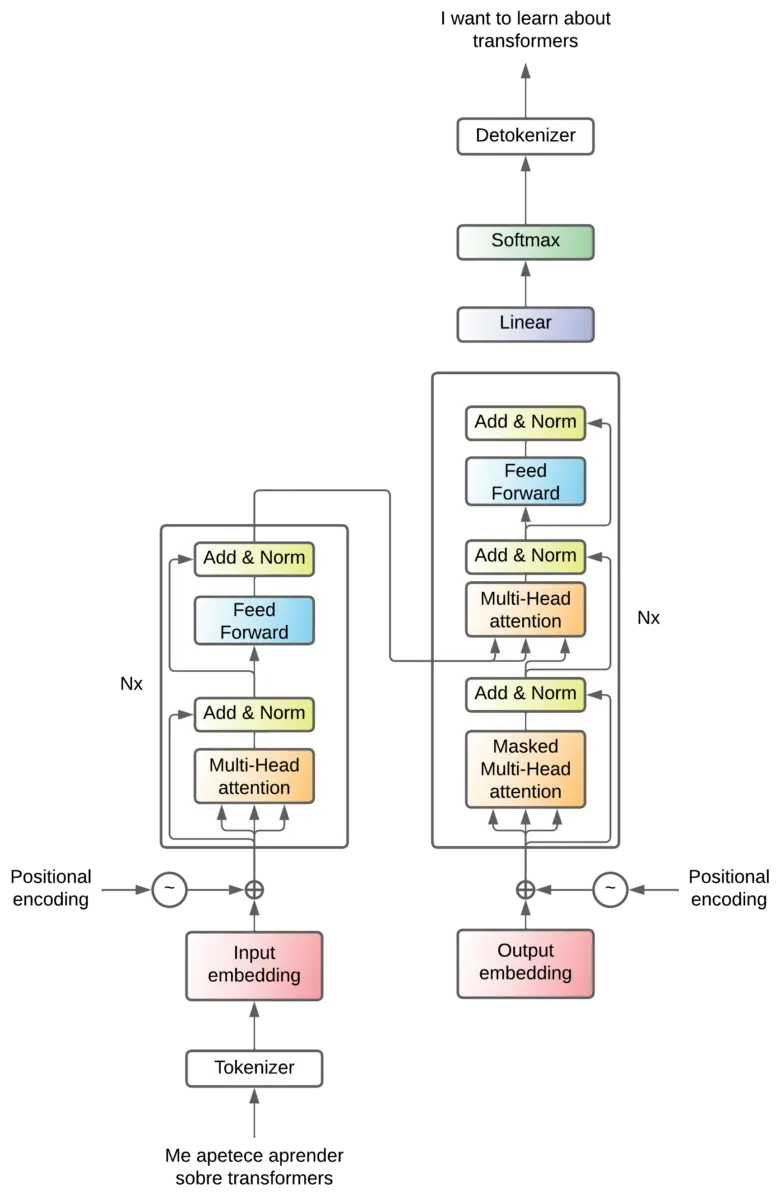
Estas son capas que se añaden después de cada capa de atención y de cada capa feed forward. Esta capa suma la salida y la entrada de una capa. A esto se llama conexiones residuales y tiene las siguientes ventajas

• Durante el entrenamiento:

  • Reducen el problema del desvanecimiento del gradiente: Cuando una red neuronal es muy grande, en el proceso de entrenamiento, los gradientes se van haciendo cada vez más pequeños según se profundizan en las capas. Esto hace que las capas más profundas no puedan actualizar bien sus pesos. Las conexiones residuales permiten el paso de los gradientes directamente a través de las capas, lo que ayuda a mantenerlos lo suficientemente grandes para que el modelo pueda seguir aprendiendo, incluso en las capas más profundas.

  • Permiten el entrenamiento de redes más profundas: Al ayudar a mitigar el problema del desvanecimiento del gradiente, las conexiones residuales también facilitan el entrenamiento de redes más profundas, lo cual puede llevar a mejor rendimiento.

• Durante la inferencia:

  • Permiten la transmisión de información entre diferentes capas: Como las conexiones residuales permiten que la salida de cada capa se convierta en la suma de la entrada y la salida de la capa, la información de la información de las capas más profundas se transmiten a las capas de más alto nivel. Esto puede ser beneficioso en muchas tareas, especialmente en las que la información de bajo y alto nivel puede ser útil.

  • Mejoran la robustez del modelo: Dado que las conexiones residuales permiten que las capas aprendan mejor en las capas más profundas, los modelos con conexiones residuales pueden ser más robustos a perturbaciones en los datos de entrada.

  • Permiten la recuperación de información perdida: Si alguna información se pierde durante la transformación en alguna capa, las conexiones residuales pueden permitir que esta información sea recuperada en las capas posteriores.

Esta capa se llama Add & Norm, hemos visto el Add, veamos el Norm. La normalización se añade para que al sumar la entrada y la salida no se disparen los valores.

Ya hemos visto todas las capas de alto nivel del transformer

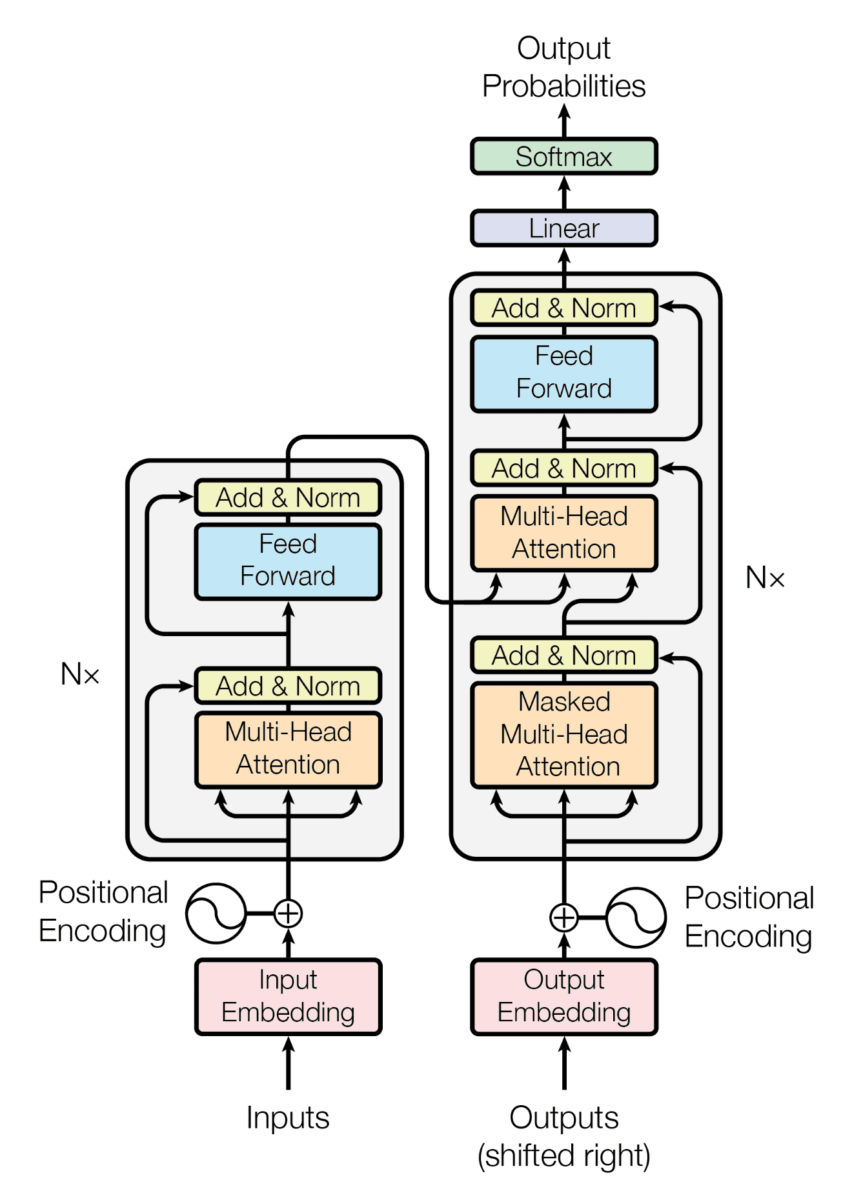
por lo que podemos entrar a ver la parte más importante y que le da nombre al paper, los mecanismos de atención

Mecanismos de atención

Multi-head attention

Antes de ver el verdadero mecanismo de atención tenemos que ver el multi-head attention

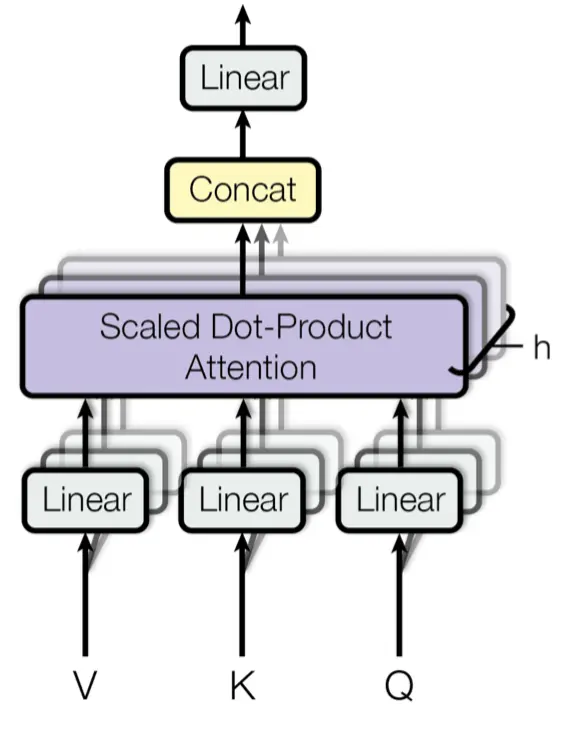
Cuando hemos explicado las capas de alto nivel, hemos visto que en las capas de atención entraban 3 flechas, estas son Q, K y V. Son matrices que corresponden a la información de los tokens, en el caso del mecanismo de atención del encoder, corresponden a los tokens de la frase del idioma original, y en el caso de la capa de atención del decoder, corresponden a los tokens de la frase que se ha traducido hasta el momento y de la salida del encoder.

En realidad ahora nos da igual el origen de los tokens, solo quédate con la idea que corresponden a tokens. Como hemos explicado los tokens se convierten a embeddings, por lo que Q, K y V son matrices de tamaño ($n_{tokens}$ x $d_{model}$). Normalmente la dimensión del embedding ($d_{model}$) suele ser un número grande, como 512, 1024, 2048, etc (no tiene por que ser una potencia de 2, son solo ejemplos).

Hemos explicado que los embeddings son representaciones vectoriales de los tokens. Es decir, los tokens se convierten a espacios vectoriales en los que las palabras con significado semántico similar están cerca.

Por tanto de todas esa dimensiones, unas pueden estar relacionadas con características morfológicas, otras con características sintácticas, otras con características semánticas, etc. Por lo que tiene sentido que se calculen los mecanismos de atención entre dimensiones de los embeddings de características similares.

Recordemos que los mecanismos de atención buscan similitud entre palabras, por lo que tiene sentido que se busque similitud entre características similares.

Es por esto, que antes de calcular los mecanismos de atención se separan las dimensiones de los embeddings en grupos de características similares, y se calculan los mecanismos de atención entre esos grupos.

¿Y cómo se hace esta separación? Habria que buscar las dimensiones similares, pero hacer esto en un espacio de 512, 1024, 2048, etc dimensiones es muy complicado. Además que no se puede saber que características son similares y que en cada caso cambiaran las características que se consideran similares.

Por lo que se utilizan proyecciones lineales para separar las dimensiones en grupos. Es decir, se pasan los embeddings por capas lineales que los separan en grupos de características similares. De esta manera, durante el entrenamiento del transformer irán cambiando los pesos de las capas lineales hasta llegar a un punto en el que la agrupación se haga de una manera óptima.

Ahora podemos tener la duda de en cuántos grupos dividir. En el paper original se dividen en 8 grupos, pero no hay ninguna razón para que sean 8, supongo que probaron varios valores y este fue el que mejor les funcionó.

Una vez se han dividido los embeddings en grupos similares y se ha calculado la atención en los distintos grupos se concatenan los resultados. Esto es lógico, supongamos que tenemos un ebedding de 512 dimensiones, y lo dividimos en 8 grupos de 64 dimensiones, si calculamos la atención en cada uno de los grupos, tendremos 8 matrices de atención 64 dimensiones, si las concatenamos tendremos una matriz de atención 512 dimensiones, que es la misma dimensión que teníamos al principio.

Pero la concatenación hace que todas las características estén juntas. Las primeras 64 dimensiones corresponden a una característica, las siguientes 64 a otra, y así sucesivamente. Así que para volver a mezclarlas se vuelve a pasar una capa lineal que mezcla todas las características. Y esa mezcla se va aprendiendo durante el entrenamiento.

Scale dot product attention

Llegamos a la parte más importante del transformer, el mecanismo de atención, el scaled dot product attention

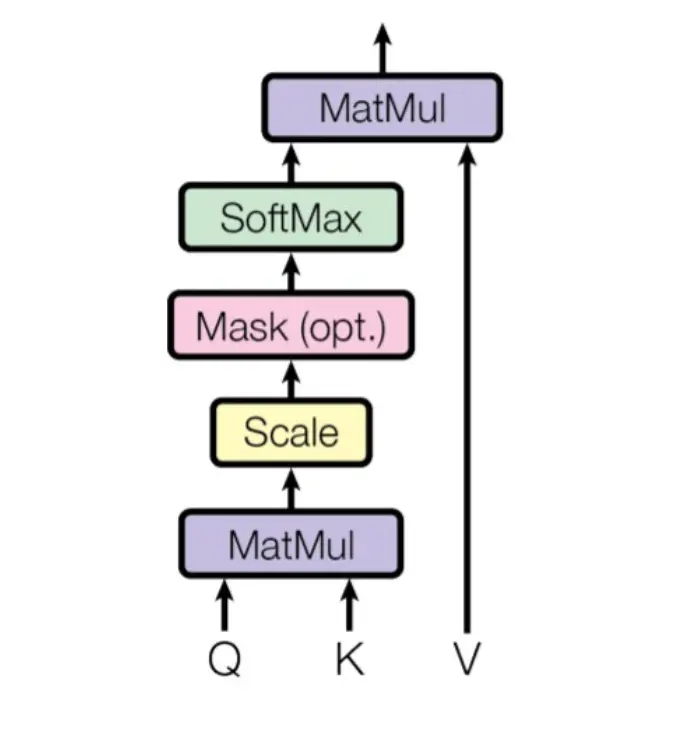
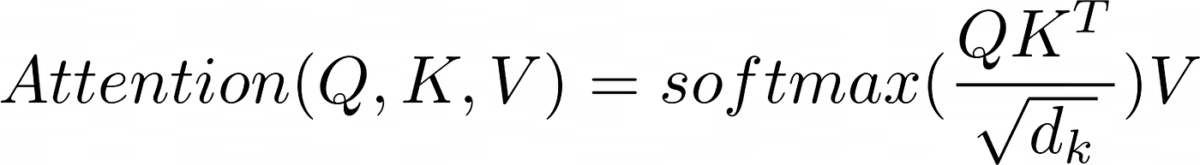
Como hemos visto, en la arquitectur del Transformer hay tres mecanismos de atención

El del encoder, el del decoder y el del encoder-decoder. Así que vamos a explicarlos por separado, porque aunque son casi iguales, tienen unas pequeñas diferencias

Endocer scale dot product attention

Vamos a ver otra vez el diagrama de bloques y la fórmula

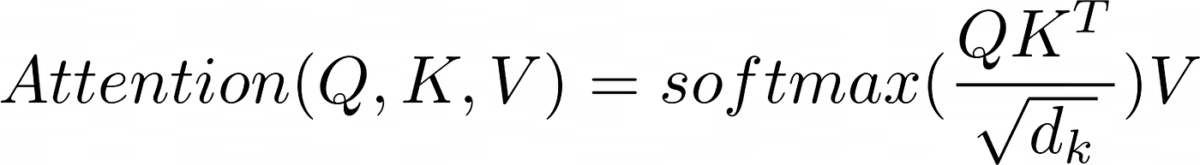
Primero vamos a entender por qué entraban tres flechas a las capas de atención. Si vemos la arquitectura del transformer, la entrada del encoder se divide en tres y entra a la capa de atención

Por lo que K, Q y V son el resultado del embedding y el positional encoding. Se mete a la capa de atención la misma matriz tres veces. Tenemos que recordar que esa matriz consistía en una lista con todos los tokens ($n_{tokens}$), y cada token se convertía en un vector de embeddings de dimensión $d_{model}$, por lo que la dimensión de la matriz será ($n_{tokens}$ x $d_{model}$).

El significao de K, Q y V proviene de las bases de datos key, query y value. Al mecanismo de atención se le pasan las matrices Q y K, es decir, se le pasa la pregunta y la clave, y a la salida se obtiene la matriz V, es decir, la respuesta.

Vamos a ver cada bloque por separado y entenderemos mejor esto

Matmul

Este bloque corresponde a la multiplicación matricial de las matrices Q y K. Pero para poder realizar esta operación hay que hacerla con la matriz transpuesta de K. Ya que como las dos matrices tienen dimensión ($n_{tokens}$ x $d_{model}$), para poder multiplicarlas, la matriz K tiene que estar traspuesta.

Por lo que tendremos una multiplicación de una matriz de dimensión ($n_{tokens}$ x $d_{model}$) por otra matriz de dimensión ($d_{model}$ x $n_{tokens}$), por lo que el resultado será una matriz de dimensión ($n_{tokens}$ x $n_{tokens}$).

Como podemos ver, el resultado es una matriz donde la diagonal es la multiplicación del embedding de cada token por si mismo, y el resto de posiciones son las multiplicaciones entre los embeddings de cada token.

Ahora vamos a ver por qué se hace esta multiplicación. En en alterior post Medida de similitud entre embeddings vimos que una manera de obtener la similitud entre dos vectores de embeddings es mediante el cálculo del coseno

En la figura anterior se puede ver que la multiplicación entre las matrices Q y K corresponde a la multiplicación de los embeddings de cada token. La multiplicación entre dos vectores se realiza de la siguiente manera

Es decir, tenemos la multiplicación de las normas por su coseno. Si los vectores fuesen unitarios, es decir, que sus normas sean 1, la multiplicación de dos vectores sería igual al coseno entre ambos vectores, que es una de las medidas de similitud entre vectores.

Por lo que como en cada posición de la matriz resultante tenemos la multiplicación entre los vectores de embeddings de cada token, en realidad, cada posición de la matriz representará la similitud entre cada token.

Recordemos lo que eran los embeddings, los embeddings eran representaciones vectoriales de los tokens en un espacio vectorial, donde los tokens con similitud semántica estan cerca.

De modo que con esta multiplicación hemos obtenido una matriz de similitud entre los tokens de la frase

Los elementos de la diagonal tienen máxima similitud (verde), los de las esqunas tienen mínima similitud (rojo), y el resto de elementos tienen similitud intermedia.

Scale

Volvemos a ver el diagrama del scaled dot product attention y su fórmula

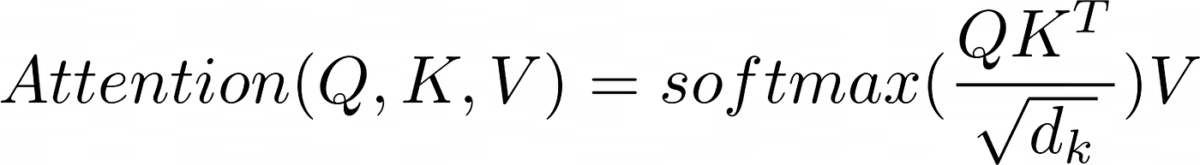
Habíamos dicho que si al multiplicar Q por K relizábamos la multiplicación entre los vectores de embeddings, y que si esos vectores tuviesen norma 1, el resultado sería la similitud entre los vectores. Pero como los vectores no tienen norma 1, el resultado puede tener valores muy altos, por lo que se normaliza dividiendo por la raíz cuadrada de la dimensión de los vectores de embeddings.

Mask (opt)

El enmascaramiento es opcional y en el encoder no se usa, por lo que de momento no lo explicamos para no liar

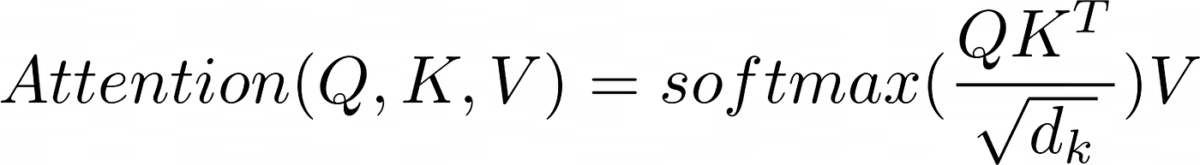
Softmax

Aunque hemos dividido por la raíz cuadrada de la dimensión de los vectores de embeddings, nos vendría muy bien que la similitud entre los vectores de embeddings vaya entre los valores 0 y 1, así que para asegurarnos eso, pasamos por una capa softmax.

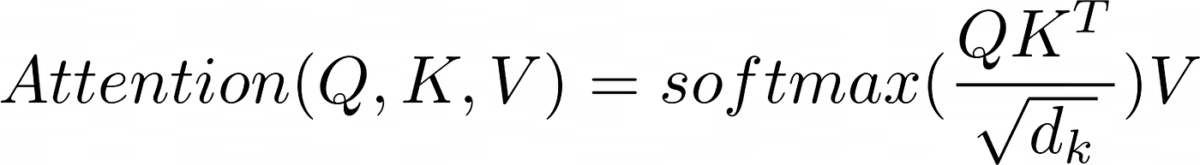
Matmul

Ahora que tenemos una matriz de similitud entre los vectores de embeddings, vamos a multiplicarla por la matriz V, que representa los embeddings de los tokens.

Haciendo la multiplicación obtenemos

Obtenemos una matriz con una mezcla de los embeddings con su similitud. En cada fila obtenemos una mezcla de los embeddings, donde cada elemento del embedding está ponderado en función de la similitud del token de esa fila con el resto de tokens.

Además volvemos a tener una matriz de tamaño ($n_{tokens}$ x $d_{model}$), que es la misma dimensión que teníamos al principio.

Resumen

En resumen, podemos decir que el scaled dot product attention es un mecanismo que calcula la similitud entre los tokens de una frase, y a partir de esa similitud, calcula una matriz de salida que corresponde a una mezcla de embeddings ponderada en función de la similitud de los tokens.

Decoder masked scale dot product attention

Volvemos a ver la arquitectura del transformer

Como vemos en este caso el scaled dot product attention tiene la palabra masked. Primero vamos a explicar el por qué de la necesidad de este enmascaramiento, y después veremos cómo se hace.

Por qué enmascarar

Como hemos dicho el transformer se ideó inicialmente como un traductor, pero en generar, es una arquitectura a la que le metes una secuencia y te saca otra secuencia. Pero a la hora del entrenamiento hay que darle la secuencia de entrada y la secuencia de salida, y a partir de ahí el transformer aprende a traducir.

Por otro lado hemos dicho que el transformer va generando un token nuevo cada vez. Es decir, se le pasa la secuencia de entrada en el encoder y un token especial de inicio de secuencia en el decoder, y a partir de ahí genera el primer token de la secuencia de salida.

A continuación se le vuelve a meter la secuencia de entrada en el encoder y el token que previamente había generado en el decoder, y a partir de ahí genera el segundo token de la secuencia de salida.

A continuación se le vuelve a meter la secuecia de entrada en el encoder y los dos tokens que previamente había generado en el decoder, y a partir de ahí genera el tercer token de la secuencia de salida.

Y así sucesivamente hasta que genera un token especial de fin de secuencia.

Pero en el entrenamiento, como se le mete la secuencia de entrada y de salida de golpe, necesitamos enmascarar los tokens que aun no ha generado para que no pueda verlos.

Mask

Vamos a ver otra vez el diagrama de bloques y la fórmula

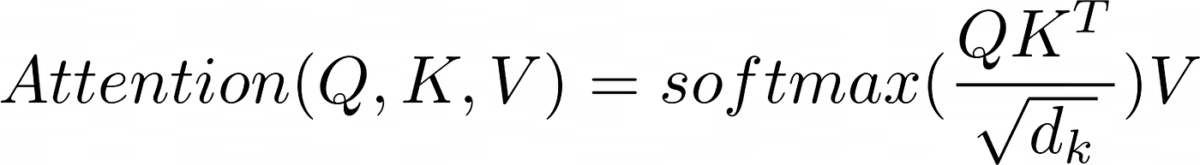
El enmascaramiento se realiza después del Scale y antes de la Softmax. Como necesitamos enmascarar los tokens "futuros" lo que se puede hacer es multiplicar la matrid resultante del Scale por una matriz que tenga 0 en las posiciones que queremos enmascarar y 1 en las que no.

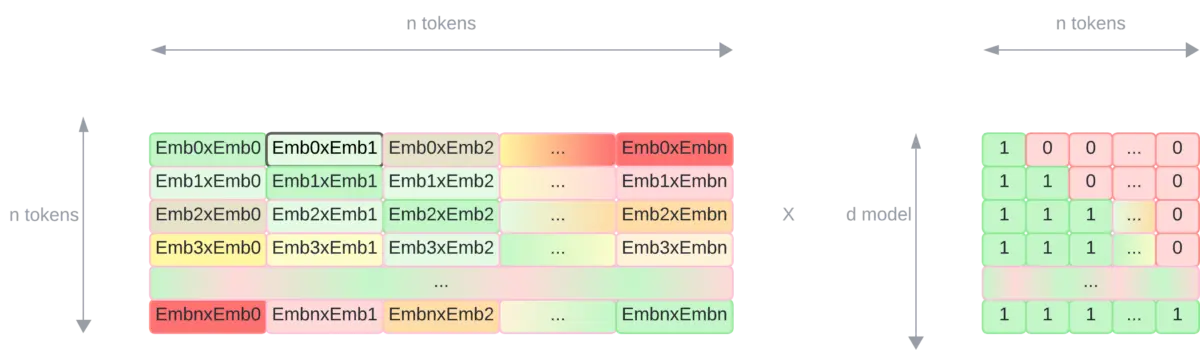
Haciendo esto obtenemos la misma matriz que antes pero con posiciones enmascaradas

Ahora el resultado del Scaled dot product attention es una matriz con los embeddings de los tokens ponderados en función de la similitud de los tokens, pero con los tokens que no se deberían ver enmascarados.

Encoder-decoder scale dot product attention

Volvemos a ver la arquitectura del transformer

Vemos ahora que al mecanismo de atención entra dos veces la salida del encoder y una vez la masked attention del decoder. Por lo que K y V son la salida del encoder, y Q es la salida del decoder.

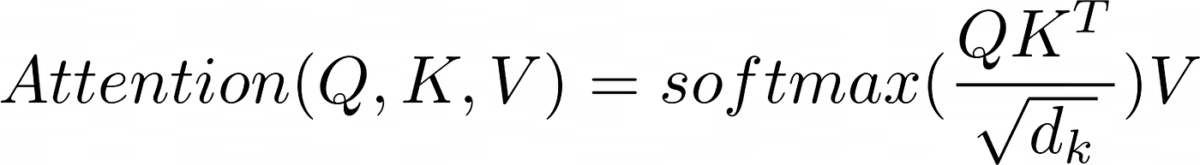
Por tanto en este bloque de atención, primero se calcula la similitud entre la sentencia del decoder y la sentencia del encoder, es decir, se calcula la similitud entre la frase que se ha traducido hasta el momento y la frase original.

A continuación se multiplica esta similitud por la sentencia del encoder, es decir, se obtiene una mezcla de los embeddings de la frase original ponderada en función de la similitud de la frase traducida hasta el momento.

Resumen

Hemos recorrido el transformer desde el más alto nivel hasta el más bajo nivel, por lo que ya puedes tener una comprensión de cómo funciona.