Ahora que hemos visto lo que son los embeddings, sabemos que podemos medir la similitud entre dos palabras midiendo la similitud entre sus embeddings. En el post de embeddings vimos el ejemplo de uso de la medida de similitud por coseno, pero existen otras medidas de similitud que podemos usar, el cuadrado L2, la similitud del producto escalar, la similitud por coseno, etc.
En este post vamos a ver estas tres que hemos mencionado
Similitud por el cuadrado L2
Esta similitud viene derivada de la distancia euclídea, que es la distancia en línea recta entre dos puntos en un espacio multidimensional, la que se calcula con el teorema de Pitágoras.
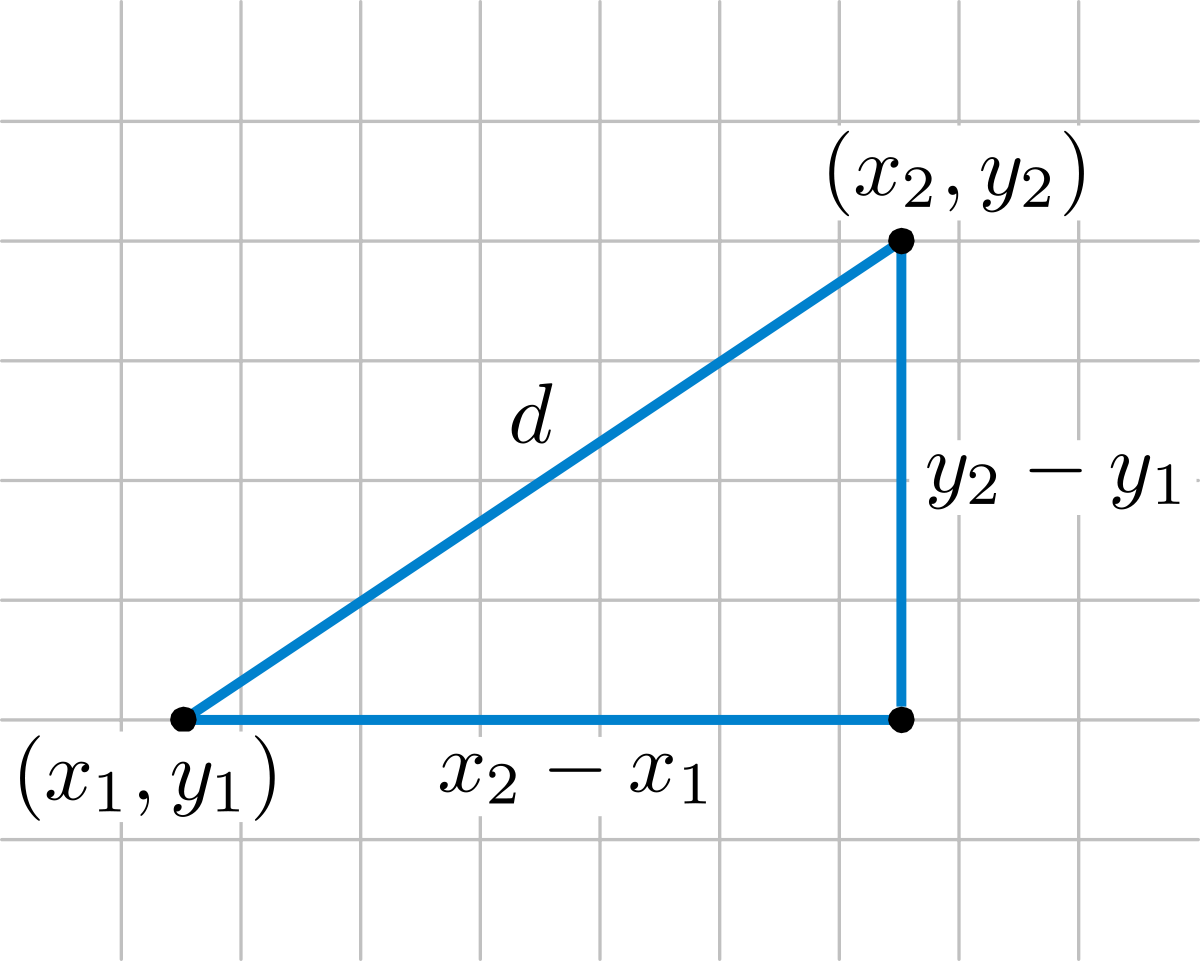
La distancia euclídea entre dos puntos p y q se calcula como:
d(p,q) = √((p1 - q1)2 + (p2 - q2)2 + ··· + (pn - qn)2) = √(∑i=1n (pi - qi)2)
La similitud por el cuadrado L2 es el cuadrado de la distancia euclídea, es decir:
similitud(p,q) = d(p,q)2 = ∑i=1n (pi - qi)2
Similitud por coseno
Si recordamos lo que aprendimos de senos y cosenos en la escuela, recordaremos que cuando dos vectores tienen un ángulo de 0º entre ellos, su coseno es 1, cuando el ángulo entre ellos es de 90º, su coseno es 0 y cuando el ángulo es de 180º, su coseno es -1.
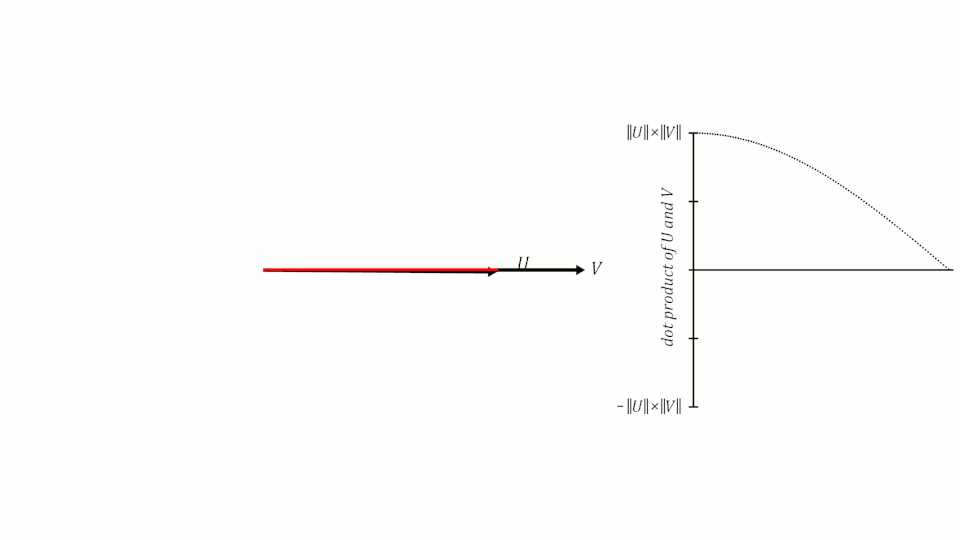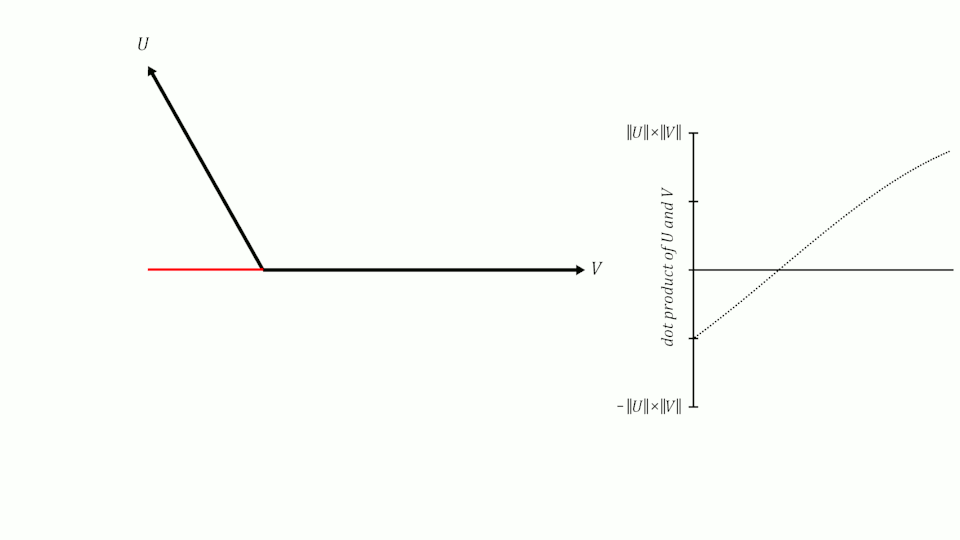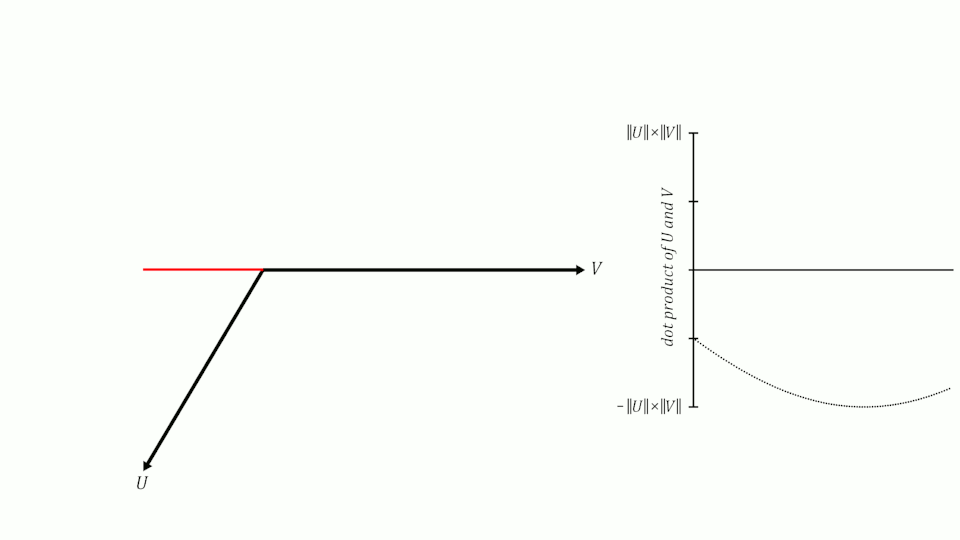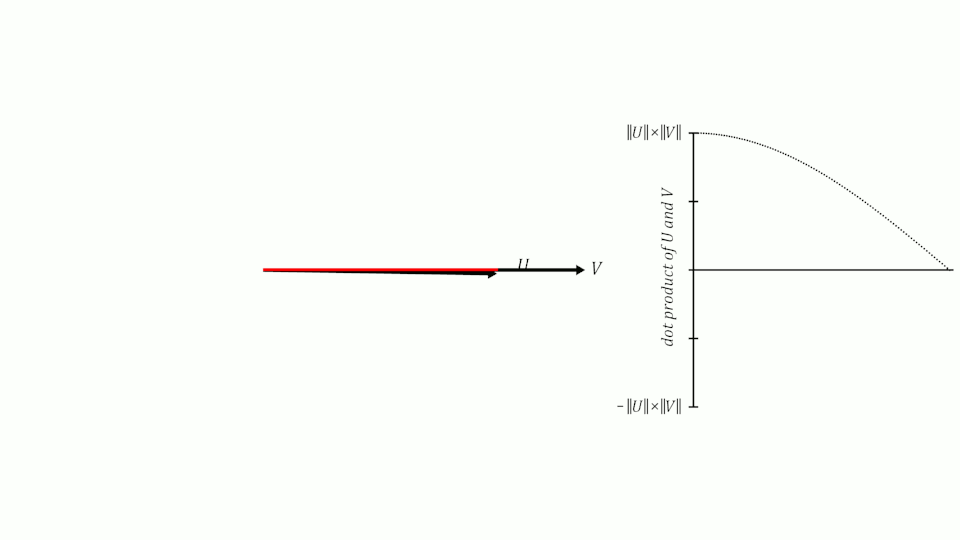
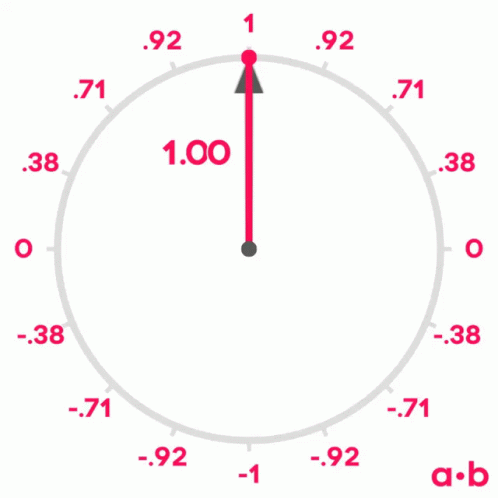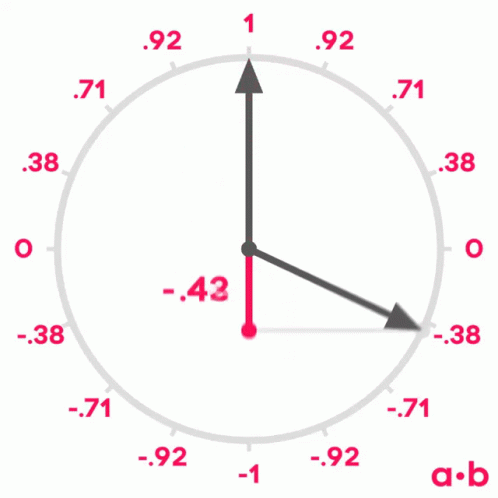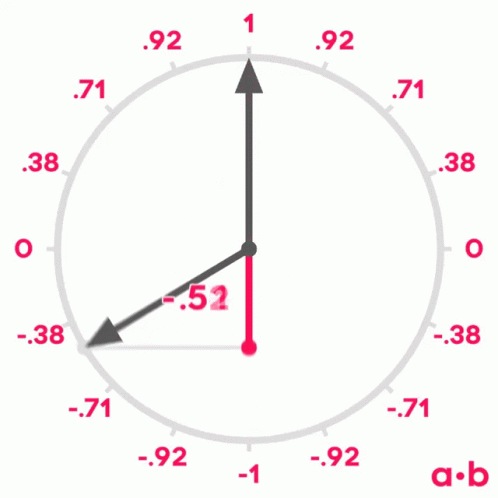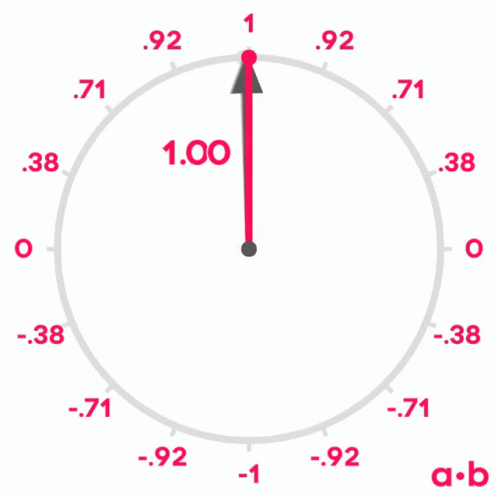
Por lo tanto, podemos usar el coseno del ángulo entre dos vectores para medir su similitud. Se puede demostrar que el coseno del ángulo entre dos vectores es igual al producto escalar de los dos vectores dividido por el producto de sus módulos. No es el objetivo de este post demostrarlo, pero si queréis podéis ver la demostración aquí.
similitud(U,V) = U · V||U|| ||V||
Similitud del producto escalar
La similitud del producto escalar es el producto escalar de dos vectores
similitud(U,V) = U · V
Como hemos escrito la fórmula de la similitud por coseno, cuando la longitud de los vectores es 1, es decir, están normalizados, la similitud por coseno es igual a la similitud del producto escalar.
Entonces, ¿Para qué nos sirve la similitud por el producto escalar? Pues para medir la similitud entre dos vectores que no están normalizados, es decir, que no tienen longitud 1.
Por ejemplo, youtube, para crear los embeddings de sus vídeos, hace que los embeddings de los vídeos que clasifica con mayor calidad sean más largos que los de los vídeos que clasifica con menor calidad.
De esta forma, cuando un usuario hace una búsqueda, la similitud por producto escalar dará mayor similitud a los vídeos de mayor calidad, por lo que le dará al usuario los vídeos de mayor calidad en primer lugar.
Qué sistema de similitud usar
Para elegir el sistema de similitud que vamos a usar, debemos tener en cuenta el espacio en el que estamos trabajando.
- Si estamos trabajando en un espacio de alta dimensionalidad, con embeddings normalizados, la similitud por coseno es la que mejor funciona. Por ejemplo OpenAI genera embeddings normalizados, por lo que la similitud por coseno es la que mejor funciona.
- Si estamos trabajando en un sistema de clasificación, donde la distancia entre dos clases es importante, la similitud por el cuadrado L2 es la que mejor funciona.
- Si estamos trabajando en un sistema de recomendación, donde la longitud de los vectores es importante, la similitud del producto escalar es la que mejor funciona.