Measure of similarity between embeddings
Now that we have seen what embeddings are, we know that we can measure the similarity between two words by measuring the similarity between their embeddings. In the embeddings post we saw the example of using the cosine similarity measure, but there are other similarity measures we can use, L2 square, scalar product similarity, cosine similarity, etc.
This notebook has been automatically translated to make it accessible to more people, please let me know if you see any typos.
In this post we are going to look at these three that we have named
Similarity by square L2
This similarity is derived from the Euclidean distance, which is the straight line distance between two points in a multidimensional space, which is calculated with the Pythagorean theorem.
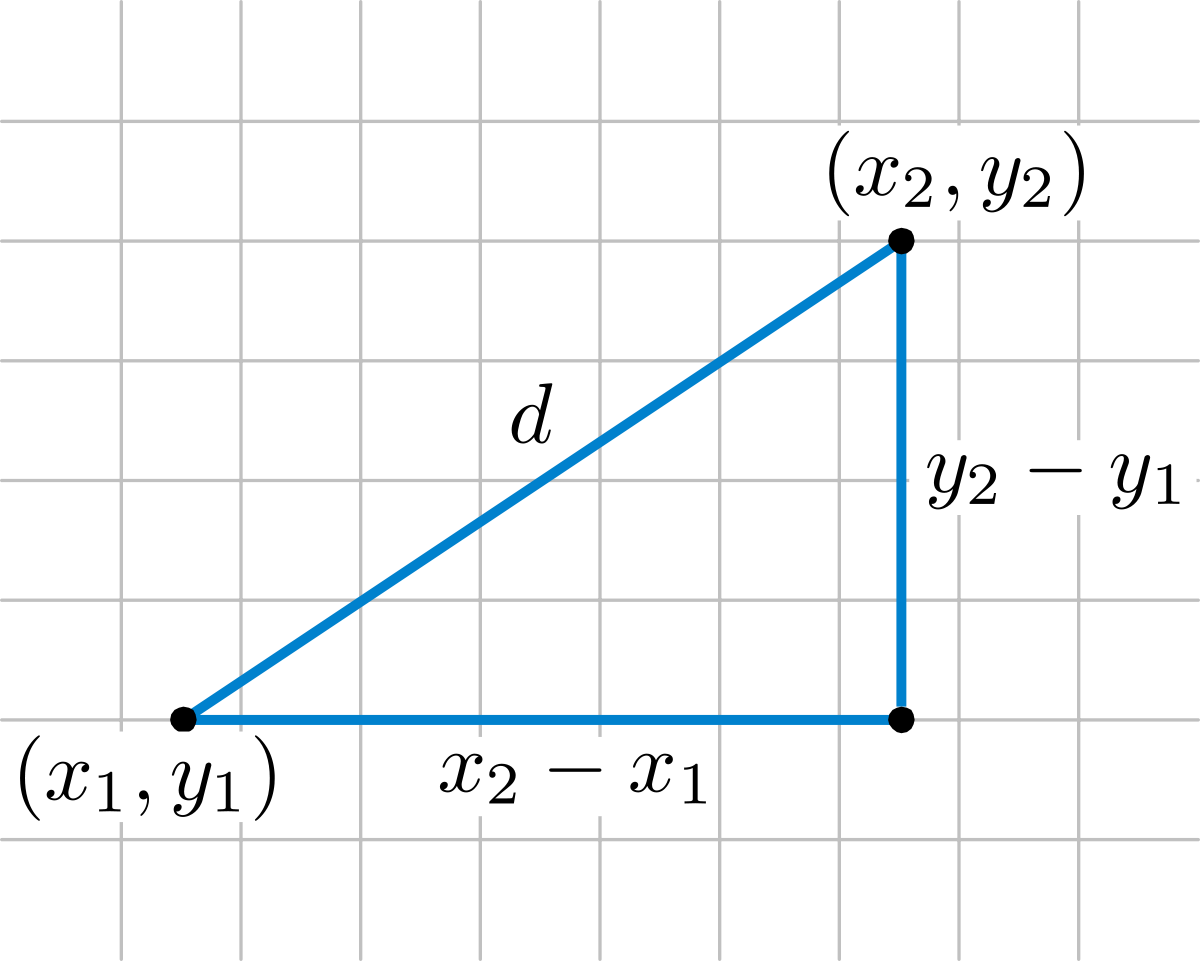
The Euclidean distance between two points $p$ and $q$ is calculated as:
$$ d(p,q) = \sqrt{(p_1 - q_1)^2 + (p_2 - q_2)^2 + \cdots + (p_n - q_n)^2} = \sqrt{{sum_{i=1}^n (p_i - q_i)^2} $$The similarity times the square L2 is the square of the Euclidean distance, that is:
$$ similarity(p,q) = d(p,q)^2 = \sum_{i=1}^n (p_i - q_i)^2 $$Cosine similarity
If we remember what we learned about sines and cosines in school, we will remember that when two vectors have an angle of 0º between them, their cosine is 1, when the angle between them is 90º, their cosine is 0 and when the angle is 180º, their cosine is -1.
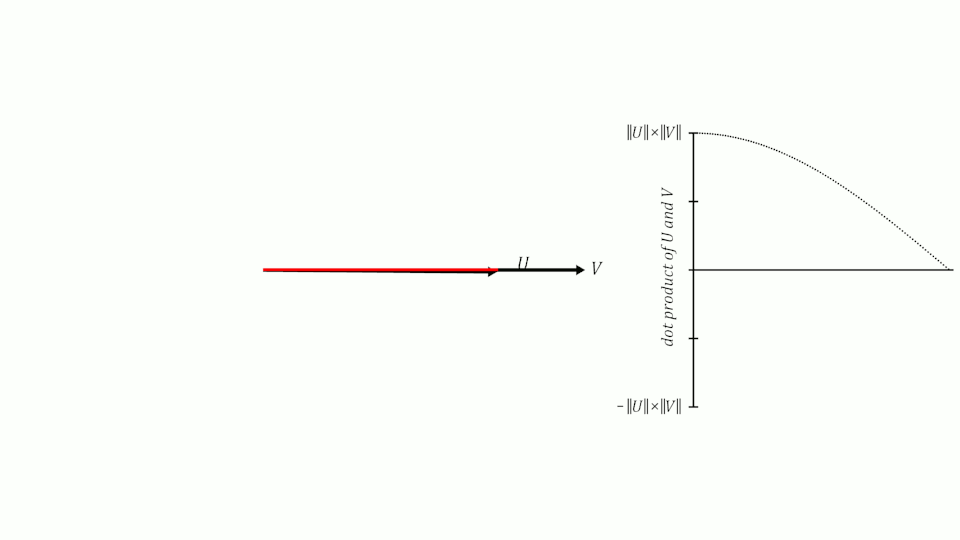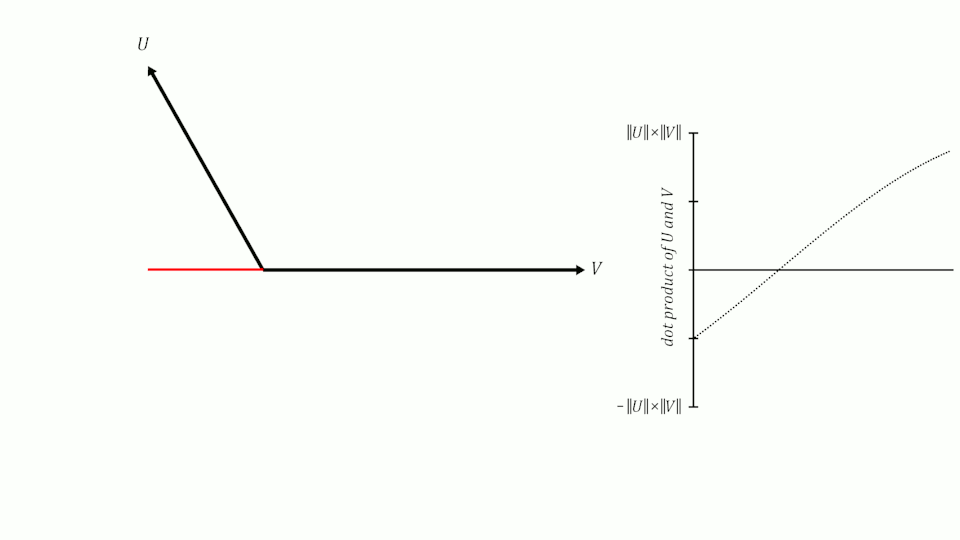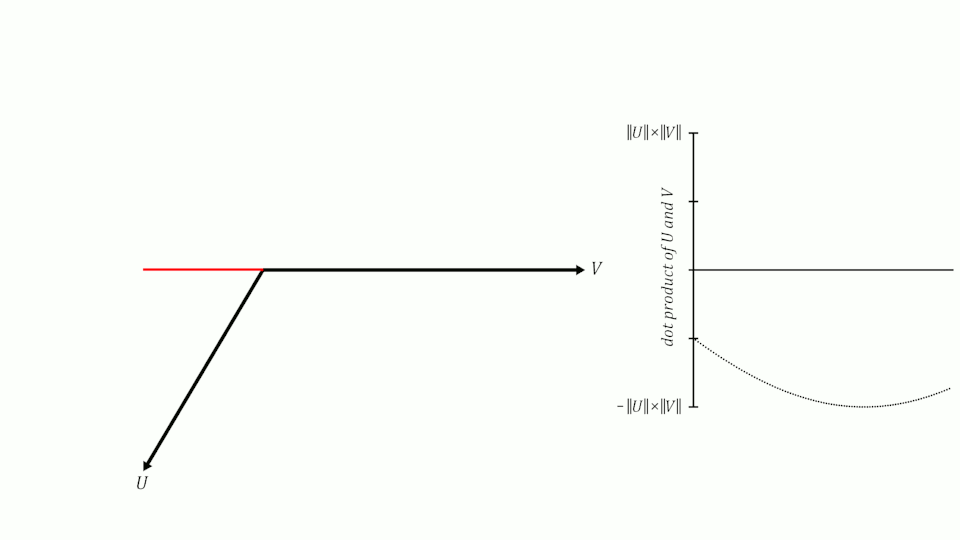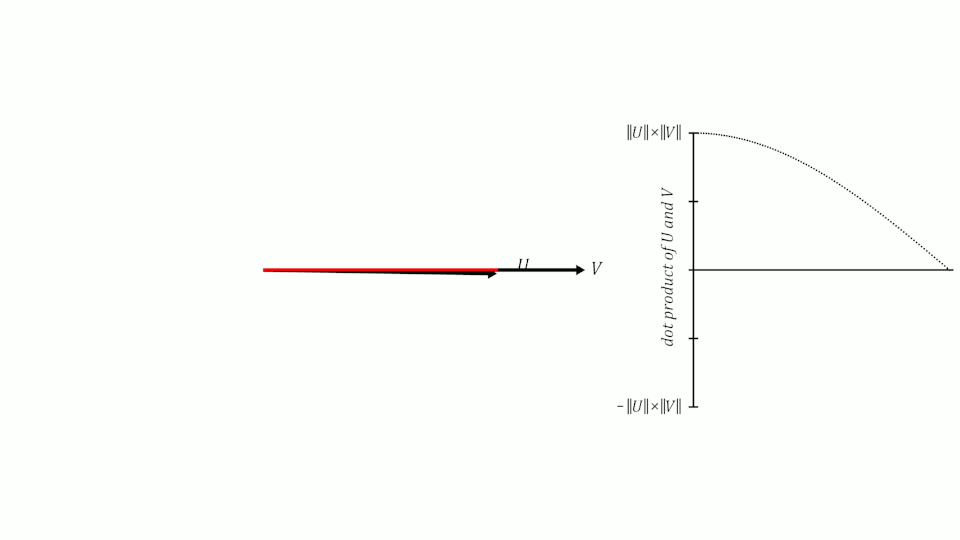
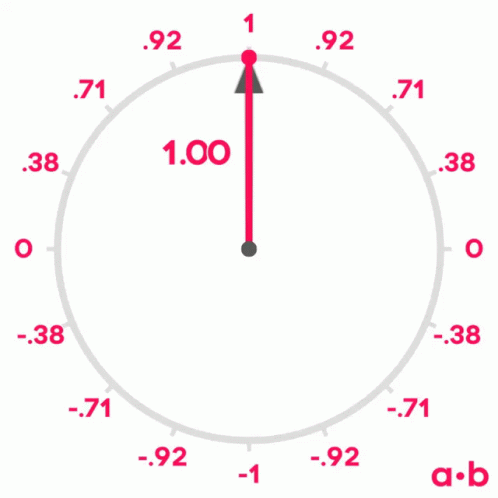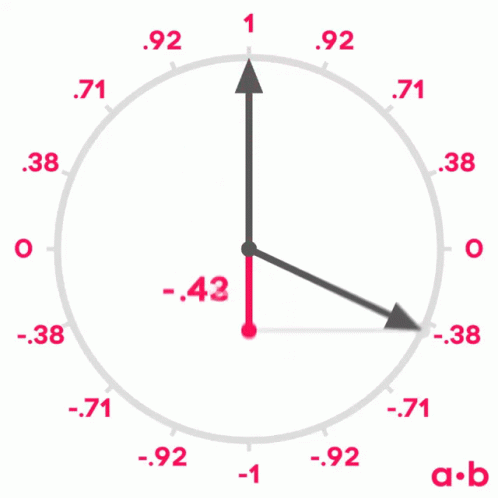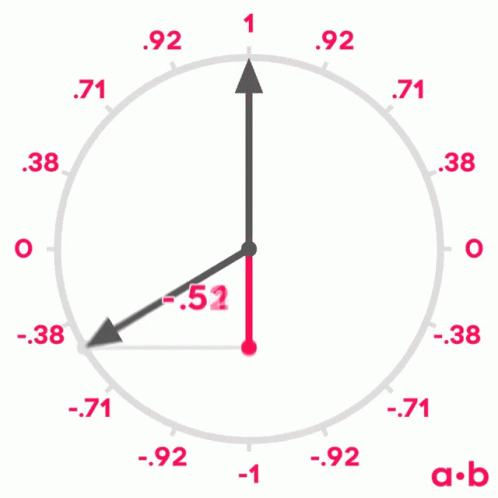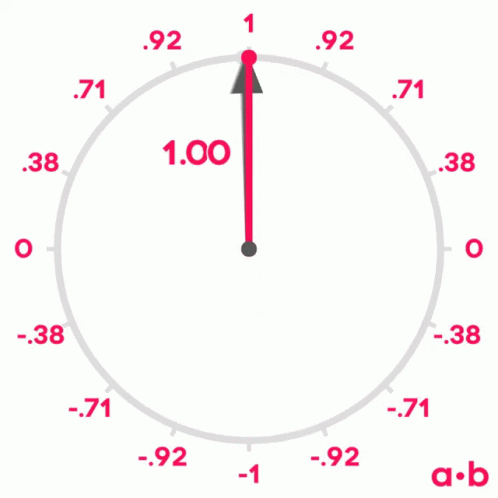
Therefore, we can use the cosine of the angle between two vectors to measure their similarity. It can be shown that the cosine of the angle between two vectors is equal to the scalar product of the two vectors divided by the product of their moduli. It is not the purpose of this post to demonstrate it, but if you want you can see the demonstration here.
$$ similarity(U,V) = \frac{U \V}{V}{V}. $$Scalar product similarity
The scalar product similarity is the scalar product of two vectors.
$$ similarity(U,V) = U \cdot V $$As we have written the cosine similarity formula, when the length of the vectors is 1, i.e., they are normalized, the cosine similarity is equal to the scalar product similarity.
So, what is the similarity by the scalar product for? Well, to measure the similarity between two vectors that are not normalized, that is, that do not have length 1.
For example, youtube, in order to create embeddings of its videos, makes the embeddings of the videos it classifies with higher quality longer than those of the videos it classifies with lower quality.
This way, when a user does a search, the similarity by product scalar will give higher similarity to higher quality videos, so it will give the user the higher quality videos first.
Which similarity system to use
To choose the similarity system we are going to use, we must take into account the space in which we are working.
- If we are working in a high dimensional space, with normalized embeddings, cosine similarity works best. For example OpenAI generates normalized embeddings, so cosine similarity works best.
- If we are working in a classification system, where the distance between two classes is important, the similarity by L2 square works best.
- If we are working in a recommender system, where the length of the vectors is important, the scalar product similarity works best.