Matrix calculation with NumPy

23 of april of 2021

Matrix calculus with NumPy

Disclaimer: This post has been translated to English using a machine translation model. Please, let me know if you find any mistakes.

1. Summary

Let's take a brief introduction to the matrix calculation library NumPy. This library is designed for all kinds of matrix calculations, so we will focus only on the part that will be useful for understanding the calculations within neural networks, but we will leave out interesting things like using the library for linear algebra.

2. What is NumPy?

NumPy is a Python library designed for performing matrix calculations. Matrix calculation is something that is widely used in science in general and in data science in particular, which is why it is necessary to have a library that does this very well.

Its name means Numerical Python

Its main object is the ndarray, which encapsulates n-dimensional arrays of homogeneous data types, unlike Python lists, which can have data of different types.

NumPy aims to perform matrix calculations much faster than with Python lists, but how is this possible?

NumPy uses compiled code, while Python uses interpreted code. The difference is that Python has to interpret, compile, and execute the code at runtime, whereas NumPy is already compiled, so it runs faster.
The ndarrays have a fixed size, unlike Python lists which are dynamic. If in NumPy you want to modify the size of an array, a new one will be created and the old one will be deleted.
All elements of ndarrays are of the same data type, unlike Python lists which can have elements of different types
Part of the NumPy code is written in C/C++ (much faster than Python)
The data in arrays is stored in memory continuously, unlike Python lists, which makes them much faster to manipulate

NumPy offers the convenience of using code that is easy to write and read, but it is written and precompiled in C, which makes it much faster.

Suppose we want to multiply two vectors, this would be done in C as follows:

for (i = 0; i < rows; i++): {
        for (j = 0; j < columns; j++): {
          c[i][j] = a[i][j]*b[i][j];
        }
      }

NumPy offers the possibility of running this code under the hood, but in a much easier way to write and understand through

c = a * b

NumPy offers vectorized code, which means you don't have to write loops, but they are still being executed underneath in optimized and precompiled C code. This has the following advantages:

The code is easier to write and read
With fewer lines of code required, there is a lower chance of introducing errors
The code looks more like mathematical notation

2.1. NumPy as `np`

Generally, when importing NumPy, it is usually imported with the alias np

	
		import numpy as np
print(np.__version__)

	
		1.18.1

3. Speed of NumPy

As explained, NumPy performs calculations much faster than Python lists. Let's look at an example where the dot product of two matrices is performed using Python lists and using ndarrays.

	
		from time import time
 
# Dimensión de las matrices
dim = 1000
shape = (dim, dim)
 
# Se crean dos ndarrays de NumPy de dimensión dim x dim
ndarray_a = np.ones(shape=shape)
ndarray_b = np.ones(shape=shape)
 
# Se crean dos listas de Python de dimensión dim x dim a partir de los ndarrays
list_a = list(ndarray_a)
list_b = list(ndarray_b)
 
# Se crean el ndarray y la lista de Python donde se guardarán los resultados
ndarray_c = np.empty(shape=shape)
list_c = list(ndarray_c)
 
# Producto escalar de dos listas de python
t0 = time()
for fila in range(dim):
  for columna in range(dim):
    list_c[fila][columna] = list_a[fila][columna] * list_b[fila][columna]
t = time()
t_listas = t-t0
print(f"Tiempo para realizar el producto escalar de dos listas de Python de dimensiones {dim}x{dim}: {t_listas:.4f} ms")
 
 
# Producto escalar de dos ndarrays de NumPy
t0 = time()
ndarray_c = ndarray_a * ndarray_b
t = time()
t_ndarrays = t-t0
print(f"Tiempo para realizar el producto escalar de dos ndarrays de NumPy de dimensiones {dim}x{dim}: {t_ndarrays:.4f} ms")
 
# Comparación de tiempos
print(f"\nHacer el cálculo con listas de Python tarda {t_listas/t_ndarrays:.2f} veces más rápido que con ndarrays de NumPy")

	
		Tiempo para realizar el producto escalar de dos listas de Python de dimensiones 1000x1000: 0.5234 ms
Tiempo para realizar el producto escalar de dos ndarrays de NumPy de dimensiones 1000x1000: 0.0017 ms
Hacer el cálculo con listas de Python tarda 316.66 veces más rápido que con ndarrays de NumPy

4. Matrices in NumPy

In NumPy an array is an ndarray object

	
		arr = np.array([1, 2, 3, 4, 5])
print(arr)
print(type(arr))

	
		[1 2 3 4 5]
<class 'numpy.ndarray'>

4.1. How to create arrays

With the array() method, you can create ndarrays by passing in Python lists (like in the previous example) or tuples.

	
		arr = np.array((1, 2, 3, 4, 5))
print(arr)
print(type(arr))

	
		[1 2 3 4 5]
<class 'numpy.ndarray'>

With the zeros() method, you can create matrices filled with zeros

	
		arr = np.zeros((3, 4))
print(arr)

	
		[[0. 0. 0. 0.]
 [0. 0. 0. 0.]
 [0. 0. 0. 0.]]

The method zeros_like(A) returns a matrix with the same shape as matrix A, but filled with zeros.

	
		A = np.array((1, 2, 3, 4, 5))
arr = np.zeros_like(A)
print(arr)

	
		[0 0 0 0 0]

With the ones() method, you can create matrices filled with ones

	
		arr = np.ones((4, 3))
print(arr)

	
		[[1. 1. 1.]
 [1. 1. 1.]
 [1. 1. 1.]
 [1. 1. 1.]]

The method ones_like(A) returns an array with the same shape as array A, but filled with ones.

	
		A = np.array((1, 2, 3, 4, 5))
arr = np.ones_like(A)
print(arr)

	
		[1 1 1 1 1]

With the empty() method, you can create arrays with the dimensions you desire, but they are initialized randomly.

	
		arr = np.empty((6, 3))
print(arr)

	
		[[4.66169180e-310 2.35541533e-312 2.41907520e-312]
 [2.14321575e-312 2.46151512e-312 2.31297541e-312]
 [2.35541533e-312 2.05833592e-312 2.22809558e-312]
 [2.56761491e-312 2.48273508e-312 2.05833592e-312]
 [2.05833592e-312 2.29175545e-312 2.07955588e-312]
 [2.14321575e-312 0.00000000e+000 0.00000000e+000]]

The method empty_like(A) returns an array with the same shape as array A, but initialized randomly.

	
		A = np.array((1, 2, 3, 4, 5))
arr = np.empty_like(A)
print(arr)

	
		[4607182418800017408 4611686018427387904 4613937818241073152
 4616189618054758400 4617315517961601024]

With the method arange(start, stop, step) you can create arrays within a specified range. This method is similar to Python's range() method.

	
		arr = np.arange(10, 30, 5)
print(arr)

	
		[10 15 20 25]

When arange is used with floating-point arguments, it is generally not possible to predict the number of elements obtained, due to the finite precision of floating-point numbers.

For this reason, it is usually better to use the function linspace(start, stop, n) which takes as an argument the number of elements we want, instead of the step.

	
		arr = np.linspace(0, 2, 9)
 
print(arr)

	
		[0.   0.25 0.5  0.75 1.   1.25 1.5  1.75 2.  ]

Lastly, if we want to create matrices with random numbers, we can use the random.rand function with a tuple containing the dimensions as a parameter.

	
		arr = np.random.rand(2, 3)
print(arr)

	
		[[0.32726085 0.65571767 0.73126697]
 [0.91938206 0.9862451  0.95033649]]

4.2. Matrix Dimensions

In NumPy we can create arrays of any dimension. To get the dimension of an array we use the ndim method.

Matrix of dimension 0, which would be equivalent to a number

	
		arr = np.array(42)
print(arr)
print(arr.ndim)

	
		42
0

1-dimensional matrix, which would be equivalent to a vector

	
		arr = np.array([1, 2, 3, 4, 5])
print(arr)
print(arr.ndim)

	
		[1 2 3 4 5]
1

2-dimensional matrix, which would be equivalent to a matrix

	
		arr = np.array([[1, 2, 3, 4, 5], 
                [6, 7, 8, 9, 10]])
print(arr)
print(arr.ndim)

	
		[[ 1  2  3  4  5]
 [ 6  7  8  9 10]]
2

Matrix of dimension 3

	
		arr = np.array([
                [[1, 2, 3, 4, 5], 
                [6, 7, 8, 9, 10]],
                
                [[11, 12, 13, 14, 15], 
                [16, 17, 18, 19, 20]]
                ])
print(arr)
print(arr.ndim)

	
		[[[ 1  2  3  4  5]
  [ 6  7  8  9 10]]
 [[11 12 13 14 15]
  [16 17 18 19 20]]]
3

Matrix of dimension N. When creating ndarrays, the number of dimensions can be set using the ndim parameter.

	
		arr = np.array([1, 2, 3, 4, 5], ndmin=6)
print(arr)
print(arr.ndim)

	
		[[[[[[1 2 3 4 5]]]]]]
6

4.3. Size of the matrices

If we want to see the size of the matrix instead of its dimension, we can use the shape method.

	
		arr = np.array([
                [[1, 2, 3, 4, 5], 
                [6, 7, 8, 9, 10]],
                
                [[11, 12, 13, 14, 15], 
                [16, 17, 18, 19, 20]]
                ])
print(arr.shape)

	
		(2, 2, 5)

5. Data Types

The data that NumPy arrays can store are the following:

i - integer
b - boolean
u - unsigned integer
f - float
c - Complex floating point
m - Timedelta
M - DateTime
O - Object
S - string
U - Unicode string
V - Fixed memory fragment for another type (void)

We can check the data type of an array using dtype

	
		arr = np.array([1, 2, 3, 4])
print(arr.dtype)
arr = np.array(['apple', 'banana', 'cherry'])
print(arr.dtype)

	
		int64
<U6

We can also create arrays specifying the data type we want them to have using dtype

	
		arr = np.array([1, 2, 3, 4], dtype='i')
print("Enteros:")
print(arr)
print(arr.dtype)
 
arr = np.array([1, 2, 3, 4], dtype='f')
print("\nFloat:")
print(arr)
print(arr.dtype)
 
arr = np.array([1, 2, 3, 4], dtype='f')
print("\nComplejos:")
print(arr)
print(arr.dtype)
 
arr = np.array([1, 2, 3, 4], dtype='S')
print("\nString:")
print(arr)
print(arr.dtype)
 
arr = np.array([1, 2, 3, 4], dtype='U')
print("\nUnicode string:")
print(arr)
print(arr.dtype)
 
arr = np.array([1, 2, 3, 4], dtype='O')
print("\nObjeto:")
print(arr)
print(arr.dtype)

	
		Enteros:
[1 2 3 4]
int32
Float:
[1. 2. 3. 4.]
float32
Complejos:
[1. 2. 3. 4.]
float32
String:
[b'1' b'2' b'3' b'4']
|S1
Unicode string:
['1' '2' '3' '4']
<U1
Objeto:
[1 2 3 4]
object

6. Mathematical Operations

6.1. Basic Operations

Matrix operations are performed element-wise, for example, if we add two matrices, the elements of each matrix in the same position will be added, just as it is done in the mathematical addition of two matrices.

	
		A = np.array([1, 2, 3])
B = np.array([1, 2, 3])
print(f"Matriz A: tamaño {A.shape}\n{A}\n")
print(f"Matriz B: tamaño {B.shape}\n{B}\n")
C = A + B
print(f"Matriz C: tamaño {C.shape}\n{C}\n")
D = A - B
print(f"Matriz D: tamaño {D.shape}\n{D}")

	
		Matriz A: tamaño (3,)
[1 2 3]
Matriz B: tamaño (3,)
[1 2 3]
Matriz C: tamaño (3,)
[2 4 6]
Matriz D: tamaño (3,)
[0 0 0]

However, if we perform the multiplication of two matrices, the multiplication of each element of the matrices (dot product) is also carried out.

	
		A = np.array([[3, 5], [4, 1]])
B = np.array([[1, 2], [-3, 0]])
 
print(f"Matriz A: tamaño {A.shape}\n{A}\n")
print(f"Matriz B: tamaño {B.shape}\n{B}\n")
 
C = A * B
print(f"Matriz C: tamaño {C.shape}\n{C}\n")

	
		Matriz A: tamaño (2, 2)
[[3 5]
 [4 1]]
Matriz B: tamaño (2, 2)
[[ 1  2]
 [-3  0]]
Matriz C: tamaño (2, 2)
[[  3  10]
 [-12   0]]

To perform the matrix product that has been taught in mathematics all along, you have to use the operator @ or the method dot.

	
		A = np.array([[3, 5], [4, 1], [6, -1]])
B = np.array([[1, 2, 3], [-3, 0, 4]])
print(f"Matriz A: tamaño {A.shape}\n{A}\n")
print(f"Matriz B: tamaño {B.shape}\n{B}\n")
C = A @ B
print(f"Matriz C: tamaño {C.shape}\n{C}\n")
D = A.dot(B)
print(f"Matriz D: tamaño {D.shape}\n{D}")

	
		Matriz A: tamaño (3, 2)
[[ 3  5]
 [ 4  1]
 [ 6 -1]]
Matriz B: tamaño (2, 3)
[[ 1  2  3]
 [-3  0  4]]
Matriz C: tamaño (3, 3)
[[-12   6  29]
 [  1   8  16]
 [  9  12  14]]
Matriz D: tamaño (3, 3)
[[-12   6  29]
 [  1   8  16]
 [  9  12  14]]

If instead of creating a new array, you want to modify an existing one, you can use the operators +=, -= or *=

	
		A = np.array([[3, 5], [4, 1]])
B = np.array([[1, 2], [-3, 0]])
print(f"Matriz A: tamaño {A.shape}\n{A}\n")
print(f"Matriz B: tamaño {B.shape}\n{B}\n")
A += B
print(f"Matriz A tras suma: tamaño {A.shape}\n{A}\n")
A -= B
print(f"Matriz A tras resta: tamaño {A.shape}\n{A}\n")
A *= B
print(f"Matriz A tras multiplicación: tamaño {A.shape}\n{A}\n")

	
		Matriz A: tamaño (2, 2)
[[3 5]
 [4 1]]
Matriz B: tamaño (2, 2)
[[ 1  2]
 [-3  0]]
Matriz A tras suma: tamaño (2, 2)
[[4 7]
 [1 1]]
Matriz A tras resta: tamaño (2, 2)
[[3 5]
 [4 1]]
Matriz A tras multiplicación: tamaño (2, 2)
[[  3  10]
 [-12   0]]

Operations can be performed on all elements of an array, thanks to a property called broadcasting, which we will explore in more detail later.

	
		A = np.array([[3, 5], [4, 1]])
 
print(f"Matriz A: tamaño {A.shape}\n{A}\n")
 
B = A * 2
print(f"Matriz B: tamaño {B.shape}\n{B}\n")
 
C = A ** 2
print(f"Matriz C: tamaño {C.shape}\n{C}\n")
 
D = 2*np.sin(A)
print(f"Matriz D: tamaño {D.shape}\n{D}")

	
		Matriz A: tamaño (2, 2)
[[3 5]
 [4 1]]
Matriz B: tamaño (2, 2)
[[ 6 10]
 [ 8  2]]
Matriz C: tamaño (2, 2)
[[ 9 25]
 [16  1]]
Matriz D: tamaño (2, 2)
[[ 0.28224002 -1.91784855]
 [-1.51360499  1.68294197]]

6.2. Functions on Matrices

As can be seen in the last calculation, NumPy offers function operators over arrays; there are a lot of functions that can be performed on arrays, such as mathematical, logical, linear algebra, etc. We show some below.

	
		A = np.array([[3, 5], [4, 1]])
print(f"A\n{A}\n")
print(f"exp(A)\n{np.exp(A)}\n")
print(f"sqrt(A)\n{np.sqrt(A)}\n")
print(f"cos(A)\n{np.cos(A)}\n")

	
		A
[[3 5]
 [4 1]]
exp(A)
[[ 20.08553692 148.4131591 ]
 [ 54.59815003   2.71828183]]
sqrt(A)
[[1.73205081 2.23606798]
 [2.         1.        ]]
cos(A)
[[-0.9899925   0.28366219]
 [-0.65364362  0.54030231]]

There are some functions that return information about the arrays, such as the mean

	
		A = np.array([[3, 5], [4, 1]])
print(f"A\n{A}\n")
print(f"A.mean()\n{A.mean()}\n")

	
		A
[[3 5]
 [4 1]]
A.mean()
3.25

However, we can obtain such information for each axis through the axis attribute. If it is 0, it is done over each column; while if it is 1, it is done over each row.

	
		A = np.array([[3, 5], [4, 1]])
 
print(f"A\n{A}\n")
 
print(f"A.mean() columnas\n{A.mean(axis=0)}\n")
print(f"A.mean() filas\n{A.mean(axis=1)}\n")

	
		A
[[3 5]
 [4 1]]
A.mean() columnas
[3.5 3. ]
A.mean() filas
[4.  2.5]

6.3. Broadcasting

Matrix operations can be performed with matrices of different dimensions. In this case, NumPy will detect this and project the smaller matrix to match the larger one.

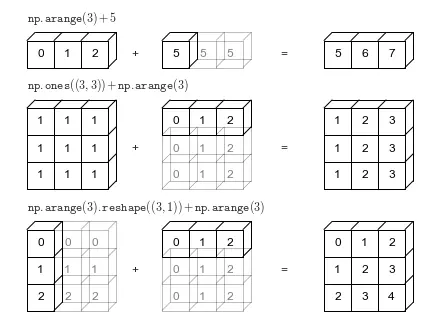
numpy_broadcasting

This is a great feature of NumPy, which allows calculations to be performed on arrays without having to worry about matching their dimensions.

	
		A = np.array([1, 2, 3])
print(f"A\n{A}\n")
B = A + 5
print(f"B\n{B}\n")

	
		A
[1 2 3]
B
[6 7 8]

	
		A = np.array([1, 2, 3])
B = np.ones((3,3))
print(f"A\n{A}\n")
print(f"B\n{B}\n")
C = A + B
print(f"C\n{C}\n")

	
		A
[1 2 3]
B
[[1. 1. 1.]
 [1. 1. 1.]
 [1. 1. 1.]]
C
[[2. 3. 4.]
 [2. 3. 4.]
 [2. 3. 4.]]

	
		A = np.array([1, 2, 3])
B = np.array([[1], [2], [3]])
 
print(f"A\n{A}\n")
print(f"B\n{B}\n")
 
C = A + B
 
print(f"C\n{C}\n")

	
		A
[1 2 3]
B
[[1]
 [2]
 [3]]
C
[[2 3 4]
 [3 4 5]
 [4 5 6]]

7. Matrix Indexing

Matrix indexing is done the same way as with Python lists

	
		arr = np.array([1, 2, 3, 4, 5])
arr[3]

In the case of having more than one dimension, the index must be specified for each of them.

	
		arr = np.array([[1, 2, 3, 4, 5], 
                [6, 7, 8, 9, 10]])
arr[1, 2]

Negative indexing can be used

	
		arr[-1, -2]

If one of the axes is not specified, it is considered that the full axis is intended.

	
		arr = np.array([[1, 2, 3, 4, 5], 
                [6, 7, 8, 9, 10]])
arr[1]

	
		array([ 6,  7,  8,  9, 10])

7.1. Slices of arrays

When indexing, we can keep parts of arrays just like we did with Python lists.

Remember that it was done as follows:

start:stop:step

Where the range goes from start (inclusive) to stop (exclusive) with a step of step

If step is not specified, it defaults to 1

For example, if we want items from the second row and from the second to the fourth column:

We select the second row with a 1 (since counting starts from 0)
We select from the second to the fourth row using 1:4, where 1 indicates the second column and 4 indicates the fifth (since the second number specifies the column where it ends without including this column). Both numbers taking into account that counting starts from 0.

	
		print(arr)
print(arr[1, 1:4])

	
		[[ 1  2  3  4  5]
 [ 6  7  8  9 10]]
[7 8 9]

We can take from a position to the end

	
		arr[1, 2:]

	
		array([ 8,  9, 10])

From the beginning to a position

	
		arr[1, :3]

	
		array([6, 7, 8])

Set the range with negative numbers

	
		arr[1, -3:-1]

	
		array([8, 9])

Choose the step

	
		arr[1, 1:4:2]

	
		array([7, 9])

7.2. Iteration over arrays

Iteration over multidimensional arrays is performed with respect to the first axis.

	
		M = np.array( [[[ 0, 1, 2],
                [ 10, 12, 13]],
               [[100,101,102],
                [110,112,113]]])
print(f'Matriz de dimensión: {M.shape}\n')
i = 0
for fila in M:
  print(f'Fila {i}: {fila}')
  i += 1

	
		Matriz de dimensión: (2, 2, 3)
Fila 0: [[ 0  1  2]
 [10 12 13]]
Fila 1: [[100 101 102]
 [110 112 113]]

However, if what we want is to iterate over each item, we can use the 'flat' method

	
		i = 0
for fila in M.flat:
  print(f'Elemento {i}: {fila}')
  i += 1

	
		Elemento 0: 0
Elemento 1: 1
Elemento 2: 2
Elemento 3: 10
Elemento 4: 12
Elemento 5: 13
Elemento 6: 100
Elemento 7: 101
Elemento 8: 102
Elemento 9: 110
Elemento 10: 112
Elemento 11: 113

8. Matrix Copying

In NumPy we have two ways to copy arrays: using copy, which makes a new copy of the array, and using view, which creates a view of the original array.

The copy owns the data and any changes made to the copy will not affect the original array, and any changes made to the original array will not affect the copy.

The view is not the owner of the data and any changes made to the copy will affect the original array, and any changes made to the original array will affect the copy.

8.1. Copy

	
		arr = np.array([1, 2, 3, 4, 5])
copy_arr = arr.copy()
arr[0] = 42
copy_arr[1] = 43
 
print(f'Original: {arr}')
print(f'Copia:    {copy_arr}')

	
		Original: [42  2  3  4  5]
Copia:    [ 1 43  3  4  5]

8.2. View

	
		arr = np.array([1, 2, 3, 4, 5])
view_arr = arr.view()
arr[0] = 42
view_arr[1] = 43
 
print(f'Original: {arr}')
print(f'Vista:    {view_arr}')

	
		Original: [42 43  3  4  5]
Vista:    [42 43  3  4  5]

8.3. Data Owner

In case of doubt whether we have a copy or a view, we can use base

	
		arr = np.array([1, 2, 3, 4, 5])
 
copy_arr = arr.copy()
view_arr = arr.view()
 
print(copy_arr.base)
print(view_arr.base)

	
		None
[1 2 3 4 5]

9. Shape of Matrices

We can know the shape of the matrix using the shape method. This will return a tuple, the size of the tuple represents the dimensions of the matrix, and each element of the tuple indicates the number of items in each of the matrix's dimensions.

	
		arr = np.array([
                [[1, 2, 3, 4, 5], 
                [6, 7, 8, 9, 10]],
                
                [[11, 12, 13, 14, 15], 
                [16, 17, 18, 19, 20]]
                ])
 
print(arr)
print(arr.shape)

	
		[[[ 1  2  3  4  5]
  [ 6  7  8  9 10]]
 [[11 12 13 14 15]
  [16 17 18 19 20]]]
(2, 2, 5)

9.1. Reshape

We can change the shape of the arrays to whatever we want using the reshape method.

For example, the previous matrix, which has a shape of (2, 2, 4). We can reshape it to (5, 4).

	
		arr_reshape = arr.reshape(5, 4)
print(arr_reshape)
print(arr_reshape.shape)

	
		[[ 1  2  3  4]
 [ 5  6  7  8]
 [ 9 10 11 12]
 [13 14 15 16]
 [17 18 19 20]]
(5, 4)

It is important to note that when resizing arrays, the number of items in the new shape must match the number of items in the original shape.

That is, in the previous example, the first array had 20 items (2x2x4), and the new array has 20 items (5x4). What we cannot do is resize it to an array of size (3, 4), since there would be a total of 12 items.

	
		arr_reshape = arr.reshape(3, 4)

	
		---------------------------------------------------------------------------
ValueError                                Traceback (most recent call last)
<ipython-input-12-29e85875d1df> in <module>()
----> 1 arr_reshape = arr.reshape(3, 4)
ValueError: cannot reshape array of size 20 into shape (3,4)

9.2. Unknown Dimension

In the case where we want to change the shape of an array and one of the dimensions is irrelevant or unknown, we can have NumPy calculate it for us by passing a -1 as the parameter.

	
		arr = np.array([
                [[1, 2, 3, 4, 5], 
                [6, 7, 8, 9, 10]],
                
                [[11, 12, 13, 14, 15], 
                [16, 17, 18, 19, 20]]
                ])
arr_reshape = arr.reshape(2, -1)
print(arr_reshape)
print(arr_reshape.shape)

	
		[[ 1  2  3  4  5  6  7  8  9 10]
 [11 12 13 14 15 16 17 18 19 20]]
(2, 10)

It's important to note that you can't put any number in the known dimensions. The number of items in the original matrix must be a multiple of the known dimensions.

In the previous example, the array has 20 items, which is a multiple of 2, the known dimension introduced. A 3 could not have been used as the known dimension, since 20 is not a multiple of 3, and there would be no number that could be placed in the unknown dimension to make the total number of items 20.

9.3. Flattening of Matrices

We can flatten the arrays, that is, convert them to a single dimension using reshape(-1). This way, regardless of the dimensions of the original array, the new one will always have a single dimension.

	
		arr = np.array([
                [[1, 2, 3, 4, 5], 
                [6, 7, 8, 9, 10]],
                
                [[11, 12, 13, 14, 15], 
                [16, 17, 18, 19, 20]]
                ])
arr_flatten = arr.reshape(-1)
print(arr_flatten)
print(arr_flatten.shape)

	
		[ 1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17 18 19 20]
(20,)

Another way to flatten an array is through the ravel() method.

	
		arr = np.array([
                [[1, 2, 3, 4, 5], 
                [6, 7, 8, 9, 10]],
                
                [[11, 12, 13, 14, 15], 
                [16, 17, 18, 19, 20]]
                ])
arr_flatten = arr.ravel()
print(arr_flatten)
print(arr_flatten.shape)

	
		[ 1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17 18 19 20]
(20,)

9.4. Transpose Matrix

The transpose of a matrix can be obtained using the method T. Transposing a matrix means swapping its rows and columns. The following image provides an example that clarifies this further.

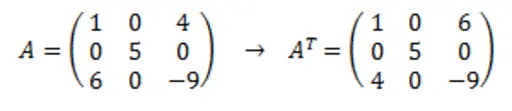
transpose_matrix

	
		arr = np.array([[1, 0, 4], 
                [0, 5, 0],
                [6, 0, -9]])
 
arr_t = arr.T
 
print(arr_t)
print(arr_t.shape)

	
		[[ 1  0  6]
 [ 0  5  0]
 [ 4  0 -9]]
(3, 3)

10. Stacking of Matrices

10.1. Vertical Stacking

Matrices can be stacked vertically (by joining rows) using the vstack() method.

	
		a = np.array([[1, 1, 1], 
              [2, 2, 2],
              [3, 3, 3]])
b = np.array([[4, 4, 4], 
              [5, 5, 5],
              [6, 6, 6]])
c = np.vstack((a,b))
c

	
		array([[1, 1, 1],
       [2, 2, 2],
       [3, 3, 3],
       [4, 4, 4],
       [5, 5, 5],
       [6, 6, 6]])

If you have matrices with more than 2 dimensions, vstack() will stack along the first dimension

	
		a = np.array([
                [[1, 1], 
                [2, 2]],
                
                [[3, 3], 
                [4, 4]]
                ])
 
b = np.array([
                [[5, 5], 
                [6, 6]],
                
                [[7, 7], 
                [8, 8]]
                ])
 
c = np.vstack((a,b))
c

	
		array([[[1, 1],
        [2, 2]],
       [[3, 3],
        [4, 4]],
       [[5, 5],
        [6, 6]],
       [[7, 7],
        [8, 8]]])

10.2. Horizontal Stacking

Matrices can be stacked horizontally (joining columns) using the hstack() method.

	
		a = np.array([[1, 2, 3], 
              [1, 2, 3],
              [1, 2, 3]])
b = np.array([[4, 5, 6], 
              [4, 5, 6],
              [4, 5, 6]])
c = np.hstack((a,b))
c

	
		array([[1, 2, 3, 4, 5, 6],
       [1, 2, 3, 4, 5, 6],
       [1, 2, 3, 4, 5, 6]])

If you have matrices with more than 2 dimensions, hstack() will stack along the second dimension.

	
		a = np.array([
                [[1, 1], 
                [2, 2]],
                
                [[3, 3], 
                [4, 4]]
                ])
b = np.array([
                [[5, 5], 
                [6, 6]],
                
                [[7, 7], 
                [8, 8]]
                ])
c = np.hstack((a,b))
c

	
		array([[[1, 1],
        [2, 2],
        [5, 5],
        [6, 6]],
       [[3, 3],
        [4, 4],
        [7, 7],
        [8, 8]]])

Another way to add columns to an array is by using the column_stack() method.

	
		a = np.array([[1, 2, 3], 
              [1, 2, 3],
              [1, 2, 3]])
 
b = np.array([4, 4, 4])
 
c = np.column_stack((a,b))
c

	
		array([[1, 2, 3, 4],
       [1, 2, 3, 4],
       [1, 2, 3, 4]])

10.3. Depth Stacking

Matrices can be stacked in depth (third dimension) using the dstack() method.

	
		a = np.array([
                [[1, 1], 
                [2, 2]],
                
                [[3, 3], 
                [4, 4]]
                ])
b = np.array([
                [[1, 1], 
                [2, 2]],
                
                [[3, 3], 
                [4, 4]]
                ])
c = np.dstack((a,b))
print(f"c: {c}\n")
print(f"a.shape: {a.shape}, b.shape: {b.shape}, c.shape: {c.shape}")

	
		c: [[[1 1 1 1]
  [2 2 2 2]]
 [[3 3 3 3]
  [4 4 4 4]]]
a.shape: (2, 2, 2), b.shape: (2, 2, 2), c.shape: (2, 2, 4)

If you have matrices with more than 4 dimensions, dstack() will stack along the third dimension.

	
		a = np.array([1, 2, 3, 4, 5], ndmin=4)
b = np.array([1, 2, 3, 4, 5], ndmin=4)
c = np.dstack((a,b))
print(f"a.shape: {a.shape}, b.shape: {b.shape}, c.shape: {c.shape}")

	
		a.shape: (1, 1, 1, 5), b.shape: (1, 1, 1, 5), c.shape: (1, 1, 2, 5)

10.3. Custom Stacking

Using the concatenate() method, you can choose the axis along which the arrays should be stacked.

	
		a = np.array([
                [[1, 1], 
                [2, 2]],
                
                [[3, 3], 
                [4, 4]]
                ])
b = np.array([
                [[5, 5], 
                [6, 6]],
                
                [[7, 7], 
                [8, 8]]
                ])
conc0 = np.concatenate((a,b), axis=0) # concatenamiento en el primer eje
conc1 = np.concatenate((a,b), axis=1) # concatenamiento en el segundo eje
conc2 = np.concatenate((a,b), axis=2) # concatenamiento en el tercer eje
print(f"conc0: {conc0}\n")
print(f"conc1: {conc1}\n")
print(f"conc2: {conc2}")

	
		conc0: [[[1 1]
  [2 2]]
 [[3 3]
  [4 4]]
 [[5 5]
  [6 6]]
 [[7 7]
  [8 8]]]
conc1: [[[1 1]
  [2 2]
  [5 5]
  [6 6]]
 [[3 3]
  [4 4]
  [7 7]
  [8 8]]]
conc2: [[[1 1 5 5]
  [2 2 6 6]]
 [[3 3 7 7]
  [4 4 8 8]]]

11. Splitting Arrays

11.1. Split Vertically

Matrices can be divided vertically (separating rows) using the vsplit() method.

	
		a = np.array([[1.1, 1.2, 1.3, 1.4], 
              [2.1, 2.2, 2.3, 2.4],
              [3.1, 3.2, 3.3, 3.4],
              [4.1, 4.2, 4.3, 4.4]])
[a1, a2] = np.vsplit(a, 2)
print(f"a1: {a1}\n")
print(f"a2: {a2}")

	
		a1: [[1.1 1.2 1.3 1.4]
 [2.1 2.2 2.3 2.4]]
a2: [[3.1 3.2 3.3 3.4]
 [4.1 4.2 4.3 4.4]]

If you have matrices with more than 2 dimensions, vsplit() will split along the first dimension.

	
		a = np.array([
                [[1, 1], 
                [2, 2]],
                
                [[3, 3], 
                [4, 4]]
                ])
[a1, a2] = np.vsplit(a, 2)
print(f"a1: {a1}\n")
print(f"a2: {a2}")

	
		a1: [[[1 1]
  [2 2]]]
a2: [[[3 3]
  [4 4]]]

11.2. Split Horizontally

Matrices can be split horizontally (separating columns) using the hsplit() method.

	
		a = np.array([[1.1, 1.2, 1.3, 1.4], 
              [2.1, 2.2, 2.3, 2.4],
              [3.1, 3.2, 3.3, 3.4],
              [4.1, 4.2, 4.3, 4.4]])
[a1, a2] = np.hsplit(a, 2)
print(f"a1: {a1}\n")
print(f"a2: {a2}")

	
		a1: [[1.1 1.2]
 [2.1 2.2]
 [3.1 3.2]
 [4.1 4.2]]
a2: [[1.3 1.4]
 [2.3 2.4]
 [3.3 3.4]
 [4.3 4.4]]

If you have matrices with more than 2 dimensions, hsplit() will split along the second dimension

	
		a = np.array([
                [[1, 1], 
                [2, 2]],
                
                [[3, 3], 
                [4, 4]]
                ])
[a1, a2] = np.hsplit(a, 2)
print(f"a1: {a1}\n")
print(f"a2: {a2}")

	
		a1: [[[1 1]]
 [[3 3]]]
a2: [[[2 2]]
 [[4 4]]]

11.3. Custom Splitting

Using the array_split() method, you can choose the axis along which to split the arrays.

	
		a = np.array([
                [[1, 1], 
                [2, 2]],
                
                [[3, 3], 
                [4, 4]]
                ])
[a1_eje0, a2_eje0] = np.array_split(a, 2, axis=0)
[a1_eje1, a2_eje1] = np.array_split(a, 2, axis=1)
[a1_eje2, a2_eje2] = np.array_split(a, 2, axis=2)
print(f"a1_eje0: {a1_eje0}\n")
print(f"a2_eje0: {a2_eje0}\n\n")
print(f"a1_eje1: {a1_eje1}\n")
print(f"a2_eje1: {a2_eje1}\n\n")
print(f"a1_eje2: {a1_eje2}\n")
print(f"a2_eje2: {a2_eje2}")

	
		a1_eje0: [[[1 1]
  [2 2]]]
a2_eje0: [[[3 3]
  [4 4]]]
a1_eje1: [[[1 1]]
 [[3 3]]]
a2_eje1: [[[2 2]]
 [[4 4]]]
a1_eje2: [[[1]
  [2]]
 [[3]
  [4]]]
a2_eje2: [[[1]
  [2]]
 [[3]
  [4]]]

12. Matrix Search

If you want to search for a value within an array, you can use the where() method which returns the positions where the array has the value we are looking for.

	
		arr = np.array([1, 2, 3, 4, 5, 4, 4])
ids = np.where(arr == 4)
ids

	
		(array([3, 5, 6]),)

Functions can be used to search, for example, if we want to find the positions where the values are even.

	
		arr = np.array([1, 2, 3, 4, 5, 6, 7, 8])
ids = np.where(arr%2)
ids

	
		(array([0, 2, 4, 6]),)

13. Sorting Arrays

By using the sort() method, we can sort arrays

	
		arr = np.array([3, 2, 0, 1])
arr_ordenado = np.sort(arr)
arr_ordenado

	
		array([0, 1, 2, 3])

If we have strings, it sorts them alphabetically

	
		arr = np.array(['banana', 'apple', 'cherry'])
arr_ordenado = np.sort(arr)
arr_ordenado

	
		array(['apple', 'banana', 'cherry'], dtype='<U6')

And it also sorts boolean arrays.

	
		arr = np.array([True, False, True])
arr_ordenado = np.sort(arr)
arr_ordenado

	
		array([False,  True,  True])

If you have matrices with more than one dimension, it sorts them by dimensions, that is, if you have a 2-dimensional matrix, it sorts the numbers in the first row among themselves and those in the second row among themselves.

	
		arr = np.array([[3, 2, 4], [5, 0, 1]])
arr_ordenado = np.sort(arr)
arr_ordenado

	
		array([[2, 3, 4],
       [0, 1, 5]])

By default, it sorts always with respect to the rows, but if you want it to sort with respect to another dimension, you have to specify it through the axis variable.

	
		arr = np.array([[3, 2, 4], [5, 0, 1]])
arr_ordenado0 = np.sort(arr, axis=0) # Se ordena con respecto a la primera dimensión
arr_ordenado1 = np.sort(arr, axis=1) # Se ordena con respecto a la segunda dimensión
print(f"arr_ordenado0: {arr_ordenado0}\n")
print(f"arr_ordenado1: {arr_ordenado1}\n")

	
		arr_ordenado0: [[3 0 1]
 [5 2 4]]
arr_ordenado1: [[2 3 4]
 [0 1 5]]

14. Filters in arrays

NumPy offers the possibility to search for certain elements in an array and create a new one

This is done by creating a boolean index array, that is, it creates a new array that indicates which positions we keep from the original array and which ones we do not.

Let's look at an example of a boolean index matrix

	
		arr = np.array([37, 85, 12, 45, 69, 22])
indices_booleanos = [False, False, True, False, False, True]
arr_filter = arr[indices_booleanos]
print(f"Array original: {arr}")
print(f"indices booleanos: {indices_booleanos}")
print(f"Array filtrado: {arr_filter}")

	
		Array original: [37 85 12 45 69 22]
indices booleanos: [False, False, True, False, False, True]
Array filtrado: [12 22]

As can be seen, the filtered array (arr_filtr), only retains the elements from the original array (arr) that correspond to those where the array indices_booleanos is True

Another thing we can see is that it has only kept the even elements, so now we will look at how to keep the even elements of an array without having to do it by hand as we did in the previous example.

	
		arr = np.array([[1, 2, 3, 4, 5], 
                [6, 7, 8, 9, 10]])
 
indices_booleanos = arr % 2 == 0
 
arr_filter = arr[indices_booleanos]
 
print(f"Array original: {arr}\n")
print(f"indices booleanos: {indices_booleanos}\n")
print(f"Array filtrado: {arr_filter}")

	
		Array original: [[ 1  2  3  4  5]
 [ 6  7  8  9 10]]
indices booleanos: [[False  True False  True False]
 [ True False  True False  True]]
Array filtrado: [ 2  4  6  8 10]

Continue reading

Langchain with open source integrations

Learn how to use Langchain with the most popular open-source integrations. In this post, we will explore how to integrate Langchain with ChromaDB, Ollama and HuggingFace.

Conventional commits

😠 ¿Tus commits parecen escritos en lenguaje alienígena? 👽 ¡Únete al club! 😅 Aprende Conventional Commits en Python y deja de torturar a tu equipo con mensajes crípticos. git-changelog y commitizen serán tus nuevos mejores amigos. 🤝

RAG fundamentals

Forget about Ctrl+F! 🤯 With RAG, your documents will answer your questions directly. 😎 Step-by-step tutorial with Hugging Face and ChromaDB. Unleash the power of AI (and show off to your friends)! 💪

Last posts -->

Have you seen these projects?

Subtify

GPU monitor

Alfred

View all projects -->

Do you want to apply AI in your project? Contact me!

Do you want to improve with these tips?

Memory profiler

See the memory usage of a script

DataLoader with pin_memory and num_workers

Increase DataLoader performance with pin_memory and num_workers

py-smi

Python library to get GPU data like `nvidia-smi`

Last tips -->

Use this locally

Hugging Face spaces allow us to run models with very simple demos, but what if the demo breaks? Or if the user deletes it? That's why I've created docker containers with some interesting spaces, to be able to use them locally, whatever happens. In fact, if you click on any project view button, it may take you to a space that doesn't work.

Flow edit

FLUX.1-RealismLora

token_hmr

View all containers -->

Do you want to apply AI in your project? Contact me!

Do you want to train your model with these datasets?

short-jokes-dataset

Dataset with jokes in English

opus100

Dataset with translations from English to Spanish

netflix_titles

Dataset with Netflix movies and series

View more datasets -->

Matrix calculus with NumPy

1. Summary

2. What is NumPy?

2.1. NumPy as np

3. Speed of NumPy

4. Matrices in NumPy

4.1. How to create arrays

4.2. Matrix Dimensions

4.3. Size of the matrices

5. Data Types

6. Mathematical Operations

6.1. Basic Operations

6.2. Functions on Matrices

6.3. Broadcasting

7. Matrix Indexing

7.1. Slices of arrays

7.2. Iteration over arrays

8. Matrix Copying

8.1. Copy

8.2. View

8.3. Data Owner

9. Shape of Matrices

9.1. Reshape

9.2. Unknown Dimension

9.3. Flattening of Matrices

9.4. Transpose Matrix

10. Stacking of Matrices

10.1. Vertical Stacking

10.2. Horizontal Stacking

10.3. Depth Stacking

10.3. Custom Stacking

11. Splitting Arrays

11.1. Split Vertically

11.2. Split Horizontally

11.3. Custom Splitting

12. Matrix Search

13. Sorting Arrays

14. Filters in arrays

Continue reading

Langchain with open source integrations

Conventional commits

RAG fundamentals

Have you seen these projects?

Do you want to apply AI in your project? Contact me!

Do you want to improve with these tips?

Memory profiler

DataLoader with pin_memory and num_workers

py-smi

Use this locally

Do you want to apply AI in your project? Contact me!

Do you want to train your model with these datasets?

short-jokes-dataset

opus100

netflix_titles

2.1. NumPy as `np`