Aviso: Este post foi traduzido para o português usando um modelo de tradução automática. Por favor, me avise se encontrar algum erro.
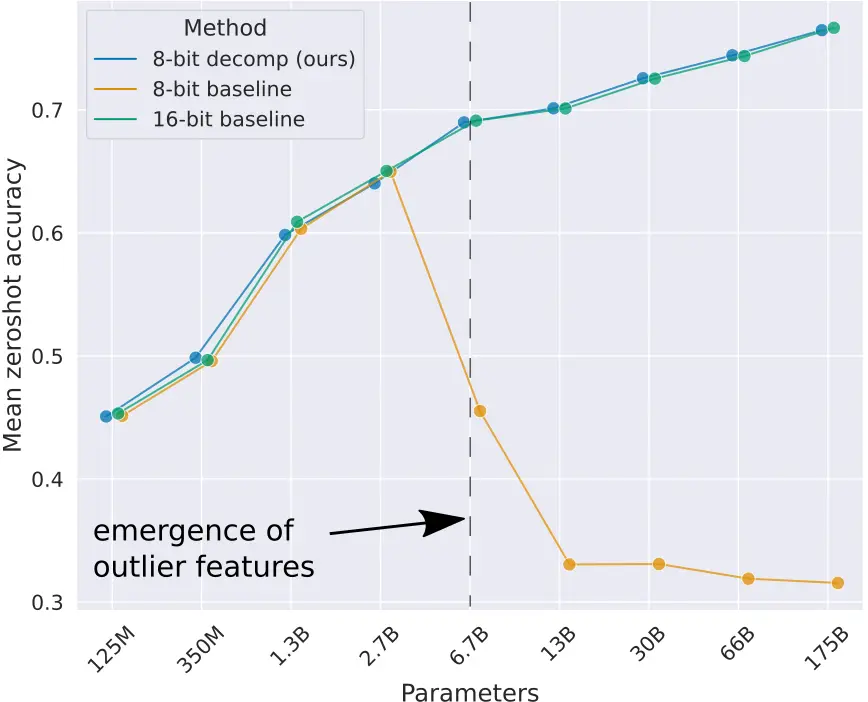
No post LLMs quantization explicamos a importância da quantização dos LLMs para economizar memória. Além disso, explicamos que existe uma maneira de quantização que é a cuantização de ponto zero que consiste em transformar os valores dos parâmetros dos pesos linearmente, mas isso tem o problema da degradação dos modelos de linguagem a partir do momento em que eles ultrapassam 2,7B de parâmetros.
Quantização vetorial
Como a quantização de todos os parâmetros dos modelos produz erro nos grandes modelos de linguagem, o que propõem no paper llm.int8() é realizar a quantização vetorial, ou seja, separar as matrizes de pesos em vetores, de maneira que alguns desses vetores podem ser quantizados em 8 bits, enquanto outros não. Portanto, os que podem ser quantizados em 8 bits são quantizados e as multiplicações matriciais são realizadas no formato INT8, enquanto os vetores que não podem ser quantizados permanecem no formato FP16 e as multiplicações são realizadas no formato FP16.
Vamos vê-lo com um exemplo
Suponhamos que temos a matriz
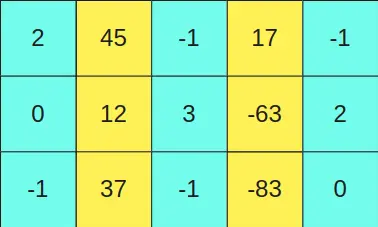
e queremos multiplicá-la pela matriz
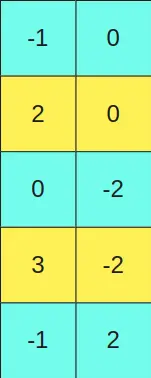
Estabelecemos um valor limiar e todas as colunas da primeira matriz que tenham um valor maior que esse limiar são deixadas no formato FP16. As linhas equivalentes às linhas da primeira matriz, na segunda matriz também são deixadas no formato FP16.
Como as colunas segunda e quarta da primeira matriz (colunas amarelas) têm valores maiores que um certo limiar, então as linhas segunda e quarta da segunda matriz (linhas amarelas) são mantidas no formato FP16.
Em caso de ter valores limiares na segunda matriz, far-se-ia o mesmo. Por exemplo, se uma linha da segunda matriz tivesse um valor maior que um limiar, ela seria deixada no formato FP16, e essa coluna na primeira matriz seria deixada no formato FP16.
O restante das linhas e colunas que não são deixadas no formato FP16 é quantizado em 8 bits e as multiplicações são realizadas no formato INT8
Então, separamos a primeira matriz em duas submatrizes
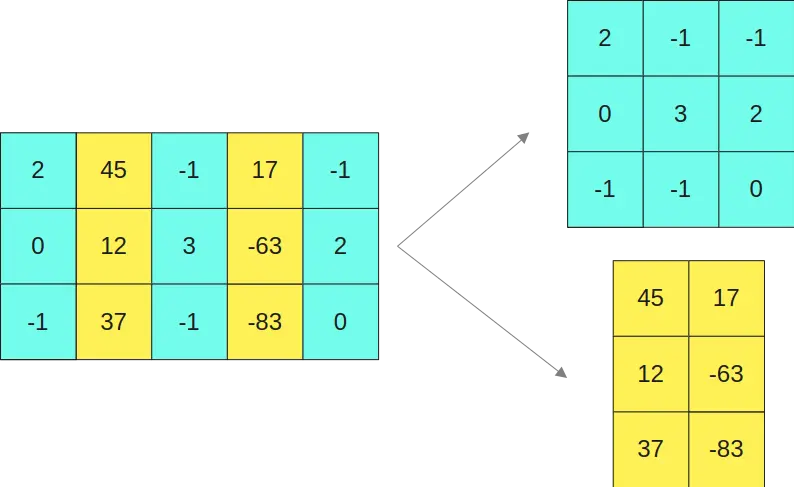
E a segunda matriz nas duas matrizes
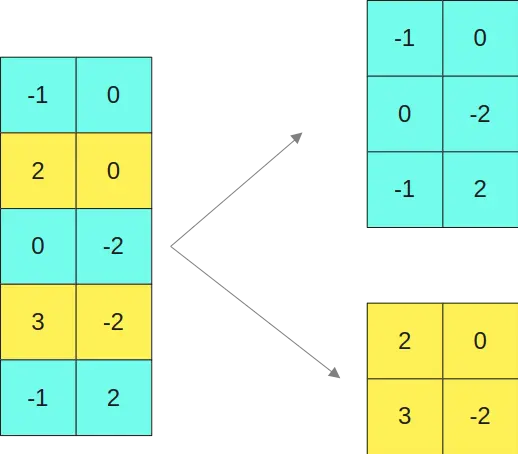
Multiplicamos as matrizes em INT8 de um lado
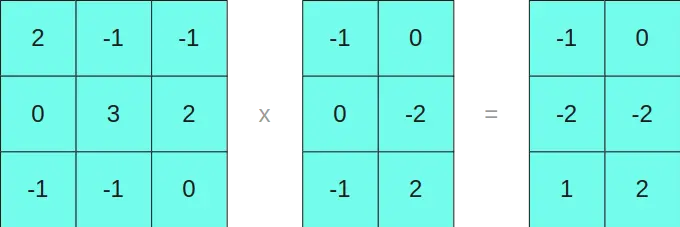
E as que estão em formato FP16 por outro lado
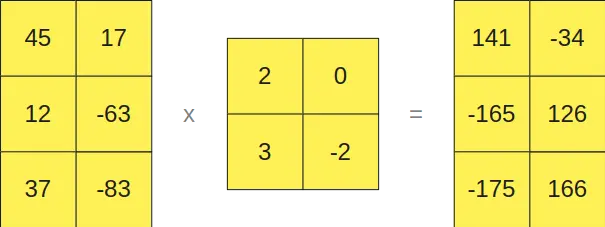
Como se pode ver, multiplicar as matrizes no formato INT8 nos dá como resultado uma matriz de tamanho 3x2, e multiplicar as matrizes no formato FP16 nos dá como resultado outra matriz de tamanho 3x2, portanto, se as somarmos
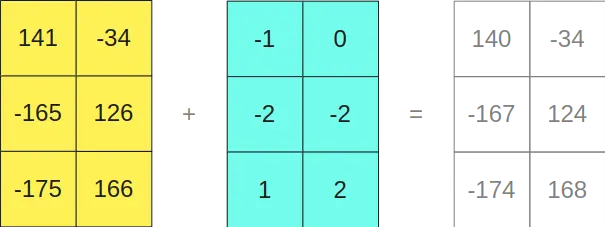
Curiosamente, nos dá o mesmo resultado que se tivéssemos multiplicado as matrizes originais
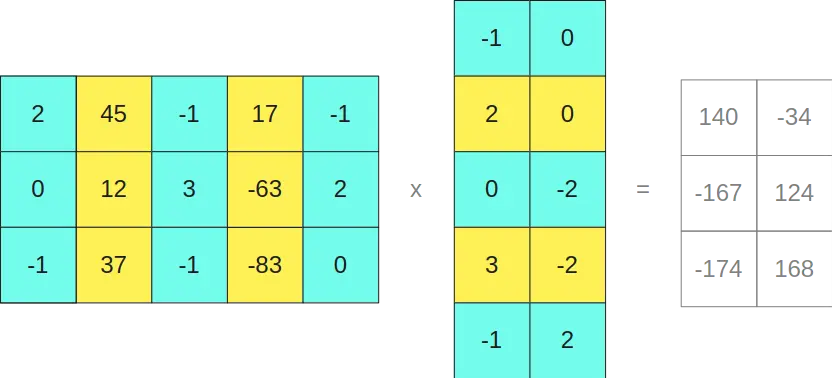
Para poder ver por que ocorre isso, se desenvolvermos o produto vetorial das duas matrizes originais
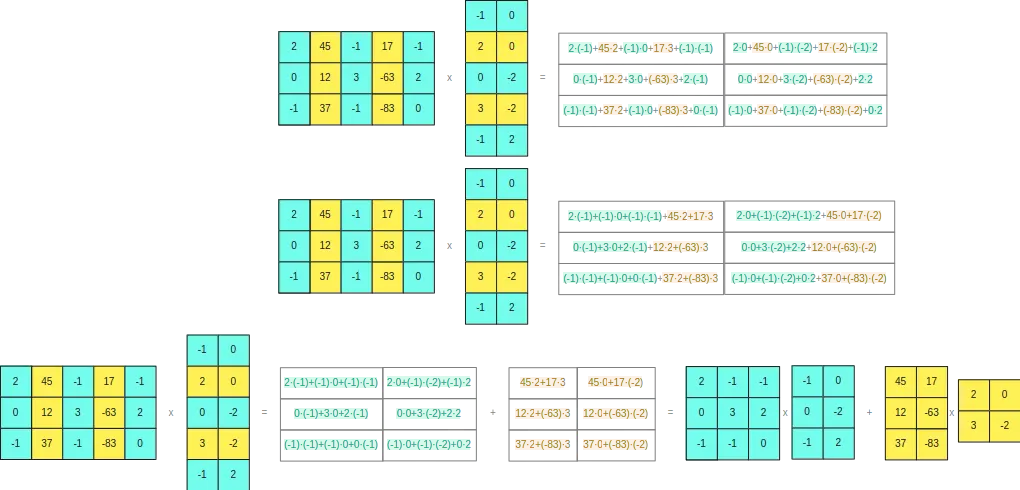
Vemos que a separação que fizemos não dá problemas
Portanto, podemos concluir que podemos separar linhas e colunas das matrizes para realizar as multiplicações matriciais. Esta separação será feita quando algum elemento da linha ou coluna seja maior que um valor limite, de maneira que as linhas ou colunas que não tenham um valor maior que esse limite serão codificadas em INT8 ocupando apenas um byte e as linhas ou colunas que tenham algum elemento maior que esse limite serão convertidas para FP16 ocupando 2 bytes. Dessa forma, não teremos problemas de arredondamento, pois os cálculos que realizarmos em INT8 serão feitos com valores que garantam que as multiplicações não ultrapassem o intervalo dos 8 bits.
Valor limiar α
Como dissem, vamos a separar em linhas e colunas que tenham algum elemento maior que um valor limiar, mas ¿qual valor limiar devemos escolher? Os autores do paper realizaram experimentos com vários valores e determinaram que esse valor limiar deveria ser α=6. Acima desse valor começaram a obter degradações nos modelos de linguagem.
Uso de llm.int8()
Vamos ver como quantizar um modelo com llm.int8() com a biblioteca transformers. Para isso, é necessário ter o bitsandbytes instalado.
pip install bitsandbytesCarregamos um modelo com 1B de parâmetros duas vezes, uma de maneira normal e a segunda quantizando-o com llm.int8()
from transformers import AutoModelForCausalLM, AutoTokenizerimport torchdevice = torch.device("cuda" if torch.cuda.is_available() else "cpu")checkpoint = "TinyLlama/TinyLlama-1.1B-Chat-v1.0"tokenizer = AutoTokenizer.from_pretrained(checkpoint)model = AutoModelForCausalLM.from_pretrained(checkpoint).to(device)model_8bit = AutoModelForCausalLM.from_pretrained(checkpoint, device_map="auto", load_in_8bit=True)Copied
The `load_in_4bit` and `load_in_8bit` arguments are deprecated and will be removed in the future versions. Please, pass a `BitsAndBytesConfig` object in `quantization_config` argument instead.
Vemos quanto memória ocupa cada um dos modelos
model.get_memory_footprint()/(1024**3), model_8bit.get_memory_footprint()/(1024**3)Copied
(4.098002195358276, 1.1466586589813232)
Como se pode ver, o modelo quantizado ocupa muito menos memória
Vamos agora fazer um teste de geração de texto com os dois modelos
input_tokens = tokenizer("Hello my name is Maximo and I am a Machine Learning Engineer", return_tensors="pt").to(device)input_tokens.input_idsCopied
tensor([[ 1, 15043, 590, 1024, 338, 5918, 4200, 322, 306, 626,263, 6189, 29257, 10863, 261]], device='cuda:0')
Vemos a saída com o modelo normal
import timet0 = time.time()max_new_tokens = 50outputs = model.generate(input_ids=input_tokens.input_ids,attention_mask=input_tokens.attention_mask,max_length=input_tokens.input_ids.shape[1] + max_new_tokens,)print(tokenizer.decode(outputs[0], skip_special_tokens=True))print(time.time() - t0)Copied
Hello my name is Maximo and I am a Machine Learning Engineer. I am currently working at [Company Name] as a Machine Learning Engineer. I have a Bachelor's degree in Computer Science from [University Name] and a Master's degree in Computer Science from [University Name]. I1.7616662979125977
E agora com o modelo quantizado
t0 = time.time()max_new_tokens = 50outputs = model_8bit.generate(input_ids=input_tokens.input_ids,attention_mask=input_tokens.attention_mask,max_length=input_tokens.input_ids.shape[1] + max_new_tokens,)print(tokenizer.decode(outputs[0], skip_special_tokens=True))print(time.time() - t0)Copied
Hello my name is Maximo and I am a Machine Learning Engineer. I am currently working at [Company Name] as a Machine Learning Engineer. I have a Bachelor's degree in Computer Science from [University Name] and a Master's degree in Computer Science from [University Name]. I9.100712776184082
Vemos duas coisas: por um lado, que na saída obtemos o mesmo texto; portanto, com um modelo muito menor podemos obter a mesma saída. No entanto, o modelo quantizado leva muito mais tempo para ser executado, então se for necessário usar esse modelo em tempo real não seria recomendável.
Isso é contraditório, porque poderíamos pensar que um modelo menor teria que ser executado mais rapidamente, mas é preciso considerar que na realidade os dois modelos, o normal e o quantizado, realizam as mesmas operações, apenas um realiza todas as operações em FP32 e o outro as faz em INT8 e FP16, no entanto, o modelo quantizado precisa encontrar linhas e colunas com valores maiores que o valor de limiar, separá-las, realizar as operações em INT8 e FP16 e depois juntar os resultados novamente, por isso o modelo quantizado leva mais tempo para ser executado.
-thumbnail.webp)