Cálculo de matriz com NumPy

23 de abril de 2021

Aviso: Este post foi traduzido para o português usando um modelo de tradução automática. Por favor, me avise se encontrar algum erro.

1. Resumo

Vamos ver uma pequena introdução à biblioteca de cálculo matricial NumPy. Esta biblioteca está projetada para todo tipo de cálculo matricial, então vamos nos concentrar apenas na parte que será útil para entender os cálculos dentro das redes neurais, deixando de lado coisas interessantes como o uso da biblioteca para a álgebra linear.

2. O que é o NumPy?

NumPy é uma biblioteca de Python projetada para realizar cálculos matriciais. O cálculo matricial é algo que se utiliza muito na ciência em geral e na ciência de dados em particular, por isso é necessário ter uma biblioteca que faça isso muito bem.

Seu nome significa Numerical Python

Seu objeto principal é o ndarray, que encapsula matrizes de dimensão n de tipos de dados homogêneos, ao contrário das listas do Python, que podem ter dados de diferentes tipos.

NumPy tem como objetivo realizar o cálculo matricial muito mais rápido do que com as listas do Python, mas como isso é possível?

NumPy utiliza código compilado, enquanto Python utiliza código interpretado. A diferença é que Python no momento da execução tem que interpretar, compilar e executar o código, enquanto NumPy já está compilado, portanto, executa mais rápido
Os ndarrays têm um tamanho fixo, ao contrário das listas do Python que são dinâmicas. Se no NumPy quiser modificar o tamanho de uma matriz, será criada uma nova e a antiga será eliminada.
Todos os elementos dos ndarrays são do mesmo tipo de dado, ao contrário das listas de Python que podem ter elementos de diferentes tipos
Parte do código do NumPy está escrita em C/C++ (muito mais rápida que Python)
Os dados das matrizes são armazenados na memória de maneira contínua, ao contrário das listas do Python, o que faz com que seja muito mais rápido manipulá-los

NumPy oferece a facilidade de usar código simples de escrever e de ler, mas que está escrito e pré-compilado em C, o que o torna muito mais rápido.

Suponhamos que queremos multiplicar dois vetores, isso seria feito em C da seguinte maneira:

for (i = 0; i < rows; i++): {
  for (j = 0; j < columns; j++): {
    c[i][j] = a[i][j]*b[i][j];
  }
}

NumPy oferece a possibilidade de executar este código por baixo, mas de uma maneira muito mais fácil de escrever e de entender através de

c = a * b

NumPy oferece código vetorizado, o que significa não ter que escrever laços, mas que, no entanto, estão sendo executados em segundo plano em código C otimizado e pré-compilado. Isso tem as seguintes vantagens:

O código é mais fácil de escrever e ler
Como são necessárias menos linhas de código, há menor probabilidade de introduzir erros
O código se assemelha mais à notação matemática

2.1. NumPy como `np`

Geralmente na hora de importar NumPy costuma-se importá-lo com o alias de np

	
		
			< >
			Input
		
		
			Python
			
		
	
	
		import numpy as np
 
print(np.__version__)
	
	Copied

>_ Output

			
				1.18.1

3. Velocidade do NumPy

Como foi explicado, o NumPy realiza o cálculo muito mais rápido do que as listas do Python. Vamos ver um exemplo no qual é realizado o produto escalar de duas matrizes, usando listas do Python e usando ndarrays.

	
		
			< >
			Input
		
		
			Python
			
		
	
	
		from time import time
 
# Dimensión de las matrices
dim = 1000
shape = (dim, dim)
 
# Se crean dos ndarrays de NumPy de dimensión dim x dim
ndarray_a = np.ones(shape=shape)
ndarray_b = np.ones(shape=shape)
 
# Se crean dos listas de Python de dimensión dim x dim a partir de los ndarrays
list_a = list(ndarray_a)
list_b = list(ndarray_b)
 
# Se crean el ndarray y la lista de Python donde se guardarán los resultados
ndarray_c = np.empty(shape=shape)
list_c = list(ndarray_c)
 
# Producto escalar de dos listas de python
t0 = time()
for fila in range(dim):
  for columna in range(dim):
    list_c[fila][columna] = list_a[fila][columna] * list_b[fila][columna]
t = time()
t_listas = t-t0
print(f"Tiempo para realizar el producto escalar de dos listas de Python de dimensiones {dim}x{dim}: {t_listas:.4f} ms")
 
 
# Producto escalar de dos ndarrays de NumPy
t0 = time()
ndarray_c = ndarray_a * ndarray_b
t = time()
t_ndarrays = t-t0
print(f"Tiempo para realizar el producto escalar de dos ndarrays de NumPy de dimensiones {dim}x{dim}: {t_ndarrays:.4f} ms")
 
# Comparación de tiempos
print(f"
Hacer el cálculo con listas de Python tarda {t_listas/t_ndarrays:.2f} veces más rápido que con ndarrays de NumPy")
	
	Copied

>_ Output

			
				Tiempo para realizar el producto escalar de dos listas de Python de dimensiones 1000x1000: 0.5234 ms
Tiempo para realizar el producto escalar de dos ndarrays de NumPy de dimensiones 1000x1000: 0.0017 ms
Hacer el cálculo con listas de Python tarda 316.66 veces más rápido que con ndarrays de NumPy

4. Matrizes em NumPy

Em NumPy, uma matriz é um objeto ndarray.

	
		
			< >
			Input
		
		
			Python
			
		
	
	
		arr = np.array([1, 2, 3, 4, 5])
 
print(arr)
print(type(arr))
	
	Copied

>_ Output

			
				[1 2 3 4 5]
&lt;class 'numpy.ndarray'&gt;

4.1. Como criar matrizes

Com o método array() é possível criar ndarrays inserindo listas do Python (como no exemplo anterior) ou tuplas

	
		
			< >
			Input
		
		
			Python
			
		
	
	
		arr = np.array((1, 2, 3, 4, 5))
 
print(arr)
print(type(arr))
	
	Copied

>_ Output

			
				[1 2 3 4 5]
&lt;class 'numpy.ndarray'&gt;

Com o método zeros() é possível criar matrizes cheias de zeros

	
		
			< >
			Input
		
		
			Python
			
		
	
	
		arr = np.zeros((3, 4))
 
print(arr)
	
	Copied

>_ Output

			
				[[0. 0. 0. 0.]
[0. 0. 0. 0.]
[0. 0. 0. 0.]]

O método zeros_like(A) retorna uma matriz com a mesma forma da matriz A, mas preenchida com zeros.

	
		
			< >
			Input
		
		
			Python
			
		
	
	
		A = np.array((1, 2, 3, 4, 5))
arr = np.zeros_like(A)
 
print(arr)
	
	Copied

>_ Output

			
				[0 0 0 0 0]

Com o método ones() é possível criar matrizes cheias de uns

	
		
			< >
			Input
		
		
			Python
			
		
	
	
		arr = np.ones((4, 3))
 
print(arr)
	
	Copied

>_ Output

			
				[[1. 1. 1.]
[1. 1. 1.]
[1. 1. 1.]
[1. 1. 1.]]

O método ones_like(A) retorna uma matriz com a mesma forma da matriz A, mas preenchida com uns.

	
		
			< >
			Input
		
		
			Python
			
		
	
	
		A = np.array((1, 2, 3, 4, 5))
arr = np.ones_like(A)
 
print(arr)
	
	Copied

>_ Output

			
				[1 1 1 1 1]

Com o método empty() podemos criar matrizes com as dimensões que desejarmos, mas inicializadas aleatoriamente.

	
		
			< >
			Input
		
		
			Python
			
		
	
	
		arr = np.empty((6, 3))
 
print(arr)
	
	Copied

>_ Output

			
				[[4.66169180e-310 2.35541533e-312 2.41907520e-312]
[2.14321575e-312 2.46151512e-312 2.31297541e-312]
[2.35541533e-312 2.05833592e-312 2.22809558e-312]
[2.56761491e-312 2.48273508e-312 2.05833592e-312]
[2.05833592e-312 2.29175545e-312 2.07955588e-312]
[2.14321575e-312 0.00000000e+000 0.00000000e+000]]

O método empty_like(A) retorna uma matriz com a mesma forma da matriz A, mas inicializada aleatoriamente.

	
		
			< >
			Input
		
		
			Python
			
		
	
	
		A = np.array((1, 2, 3, 4, 5))
arr = np.empty_like(A)
 
print(arr)
	
	Copied

>_ Output

			
				[4607182418800017408 4611686018427387904 4613937818241073152
4616189618054758400 4617315517961601024]

Com o método arange(start, stop, step) é possível criar matrizes em um intervalo determinado. Este método é semelhante ao método range() do Python.

	
		
			< >
			Input
		
		
			Python
			
		
	
	
		arr = np.arange(10, 30, 5)
 
print(arr)
	
	Copied

>_ Output

			
				[10 15 20 25]

Quando arange é usado com argumentos de ponto flutuante, geralmente não é possível prever o número de elementos obtidos, devido à precisão de ponto flutuante ser finita.

Por esse motivo, é geralmente melhor usar a função linspace(start, stop, n) que recebe como argumento a quantidade de elementos que desejamos, em vez do passo.

	
		
			< >
			Input
		
		
			Python
			
		
	
	
		arr = np.linspace(0, 2, 9)
 
print(arr)
	
	Copied

>_ Output

			
				[0.   0.25 0.5  0.75 1.   1.25 1.5  1.75 2.  ]

Por último, se quisermos criar matrizes com números aleatórios, podemos usar a função random.rand com uma tupla com as dimensões como parâmetro.

	
		
			< >
			Input
		
		
			Python
			
		
	
	
		arr = np.random.rand(2, 3)
 
print(arr)
	
	Copied

>_ Output

			
				[[0.32726085 0.65571767 0.73126697]
[0.91938206 0.9862451  0.95033649]]

4.2. Dimensões das matrizes

Em NumPy podemos criar matrizes de qualquer dimensão. Para obter a dimensão de um array usamos o método ndim

Matriz de dimensão 0, o que equivaleria a um número

	
		
			< >
			Input
		
		
			Python
			
		
	
	
		arr = np.array(42)
 
print(arr)
print(arr.ndim)
	
	Copied

>_ Output

			
				42
0

Matriz de dimensão 1, o que equivaleria a um vetor

	
		
			< >
			Input
		
		
			Python
			
		
	
	
		arr = np.array([1, 2, 3, 4, 5])
 
print(arr)
print(arr.ndim)
	
	Copied

>_ Output

			
				[1 2 3 4 5]
1

Matriz de dimensão 2, o que equivaleria a uma matriz

	
		
			< >
			Input
		
		
			Python
			
		
	
	
		arr = np.array([[1, 2, 3, 4, 5],
                [6, 7, 8, 9, 10]])
 
print(arr)
print(arr.ndim)
	
	Copied

>_ Output

			
				[[ 1  2  3  4  5]
[ 6  7  8  9 10]]
2

Matriz de dimensão 3

	
		
			< >
			Input
		
		
			Python
			
		
	
	
		arr = np.array([
                [[1, 2, 3, 4, 5],
                [6, 7, 8, 9, 10]],
                
                [[11, 12, 13, 14, 15],
                [16, 17, 18, 19, 20]]
                ])
 
print(arr)
print(arr.ndim)
	
	Copied

>_ Output

			
				[[[ 1  2  3  4  5]
  [ 6  7  8  9 10]]
[[11 12 13 14 15]
  [16 17 18 19 20]]]
3

Matriz de dimensão N. Na hora de criar ndarrays, pode-se estabelecer o número de dimensões por meio do parâmetro ndim.

	
		
			< >
			Input
		
		
			Python
			
		
	
	
		arr = np.array([1, 2, 3, 4, 5], ndmin=6)
 
print(arr)
print(arr.ndim)
	
	Copied

>_ Output

			
				[[[[[[1 2 3 4 5]]]]]]
6

4.3. Tamanho das matrizes

Se quisermos ver o tamanho da matriz em vez de sua dimensão, podemos usar o método shape

	
		
			< >
			Input
		
		
			Python
			
		
	
	
		arr = np.array([
                [[1, 2, 3, 4, 5],
                [6, 7, 8, 9, 10]],
                
                [[11, 12, 13, 14, 15],
                [16, 17, 18, 19, 20]]
                ])
 
print(arr.shape)
	
	Copied

>_ Output

			
				(2, 2, 5)

5. Tipo de dados

Os dados que as matrizes do NumPy podem armazenar são os seguintes:

i - inteiro
b - booleano
u - inteiro sem sinal
f - flutuante
c - Complexo de ponto flutuante
m - Timedelta
M - DataHora
O - Objeto
S - string
U - String de Unicode
V - Fragmento de memória fixo para outro tipo (void)

Podemos verificar o tipo de dados de uma matriz usando dtype

	
		
			< >
			Input
		
		
			Python
			
		
	
	
		arr = np.array([1, 2, 3, 4])
print(arr.dtype)
 
arr = np.array(['apple', 'banana', 'cherry'])
print(arr.dtype)
	
	Copied

>_ Output

			
				int64
&lt;U6

Também podemos criar matrizes indicando o tipo de dado que queremos que tenha através de dtype

	
		
			< >
			Input
		
		
			Python
			
		
	
	
		arr = np.array([1, 2, 3, 4], dtype='i')
print("Enteros:")
print(arr)
print(arr.dtype)
 
arr = np.array([1, 2, 3, 4], dtype='f')
print("
Float:")
print(arr)
print(arr.dtype)
 
arr = np.array([1, 2, 3, 4], dtype='f')
print("
Complejos:")
print(arr)
print(arr.dtype)
 
arr = np.array([1, 2, 3, 4], dtype='S')
print("
String:")
print(arr)
print(arr.dtype)
 
arr = np.array([1, 2, 3, 4], dtype='U')
print("
Unicode string:")
print(arr)
print(arr.dtype)
 
arr = np.array([1, 2, 3, 4], dtype='O')
print("
Objeto:")
print(arr)
print(arr.dtype)
	
	Copied

>_ Output

			
				Enteros:
[1 2 3 4]
int32
Float:
[1. 2. 3. 4.]
float32
Complejos:
[1. 2. 3. 4.]
float32
String:
[b'1' b'2' b'3' b'4']
|S1
Unicode string:
['1' '2' '3' '4']
&lt;U1
Objeto:
[1 2 3 4]
object

6. Operações matemáticas

6.1. Operações básicas

As operações matriciais são realizadas elemento a elemento, por exemplo, se somarmos duas matrizes, serão somados os elementos de cada matriz na mesma posição, assim como é feito na soma matemática de duas matrizes.

	
		
			< >
			Input
		
		
			Python
			
		
	
	
		A = np.array([1, 2, 3])
B = np.array([1, 2, 3])
 
print(f"Matriz A: tamaño {A.shape}
{A}
")
print(f"Matriz B: tamaño {B.shape}
{B}
")
 
C = A + B
print(f"Matriz C: tamaño {C.shape}
{C}
")
 
D = A - B
print(f"Matriz D: tamaño {D.shape}
{D}")
	
	Copied

>_ Output

			
				Matriz A: tamaño (3,)
[1 2 3]
Matriz B: tamaño (3,)
[1 2 3]
Matriz C: tamaño (3,)
[2 4 6]
Matriz D: tamaño (3,)
[0 0 0]

No entanto, se fizermos a multiplicação de duas matrizes, também é feita a multiplicação de cada elemento das matrizes (produto escalar).

	
		
			< >
			Input
		
		
			Python
			
		
	
	
		A = np.array([[3, 5], [4, 1]])
B = np.array([[1, 2], [-3, 0]])
 
print(f"Matriz A: tamaño {A.shape}
{A}
")
print(f"Matriz B: tamaño {B.shape}
{B}
")
 
C = A * B
print(f"Matriz C: tamaño {C.shape}
{C}
")
	
	Copied

>_ Output

			
				Matriz A: tamaño (2, 2)
[[3 5]
[4 1]]
Matriz B: tamaño (2, 2)
[[ 1  2]
[-3  0]]
Matriz C: tamaño (2, 2)
[[  3  10]
[-12   0]]

Para fazer o produto matricial que tem sido ensinado em matemática há toda a vida, é necessário usar o operador @ ou o método dot.

	
		
			< >
			Input
		
		
			Python
			
		
	
	
		A = np.array([[3, 5], [4, 1], [6, -1]])
B = np.array([[1, 2, 3], [-3, 0, 4]])
 
print(f"Matriz A: tamaño {A.shape}
{A}
")
print(f"Matriz B: tamaño {B.shape}
{B}
")
 
C = A @ B
print(f"Matriz C: tamaño {C.shape}
{C}
")
 
D = A.dot(B)
print(f"Matriz D: tamaño {D.shape}
{D}")
	
	Copied

>_ Output

			
				Matriz A: tamaño (3, 2)
[[ 3  5]
[ 4  1]
[ 6 -1]]
Matriz B: tamaño (2, 3)
[[ 1  2  3]
[-3  0  4]]
Matriz C: tamaño (3, 3)
[[-12   6  29]
[  1   8  16]
[  9  12  14]]
Matriz D: tamaño (3, 3)
[[-12   6  29]
[  1   8  16]
[  9  12  14]]

Se quisermos modificar uma matriz existente em vez de criar uma nova, podemos usar os operadores +=, -= ou *=.

	
		
			< >
			Input
		
		
			Python
			
		
	
	
		A = np.array([[3, 5], [4, 1]])
B = np.array([[1, 2], [-3, 0]])
 
print(f"Matriz A: tamaño {A.shape}
{A}
")
print(f"Matriz B: tamaño {B.shape}
{B}
")
 
A += B
print(f"Matriz A tras suma: tamaño {A.shape}
{A}
")
 
A -= B
print(f"Matriz A tras resta: tamaño {A.shape}
{A}
")
 
A *= B
print(f"Matriz A tras multiplicación: tamaño {A.shape}
{A}
")
	
	Copied

>_ Output

			
				Matriz A: tamaño (2, 2)
[[3 5]
[4 1]]
Matriz B: tamaño (2, 2)
[[ 1  2]
[-3  0]]
Matriz A tras suma: tamaño (2, 2)
[[4 7]
[1 1]]
Matriz A tras resta: tamaño (2, 2)
[[3 5]
[4 1]]
Matriz A tras multiplicación: tamaño (2, 2)
[[  3  10]
[-12   0]]

Operações podem ser realizadas em todos os elementos de uma matriz, isso é possível graças a uma propriedade chamada broadcasting que veremos com mais detalhes posteriormente.

	
		
			< >
			Input
		
		
			Python
			
		
	
	
		A = np.array([[3, 5], [4, 1]])
 
print(f"Matriz A: tamaño {A.shape}
{A}
")
 
B = A * 2
print(f"Matriz B: tamaño {B.shape}
{B}
")
 
C = A ** 2
print(f"Matriz C: tamaño {C.shape}
{C}
")
 
D = 2*np.sin(A)
print(f"Matriz D: tamaño {D.shape}
{D}")
	
	Copied

>_ Output

			
				Matriz A: tamaño (2, 2)
[[3 5]
[4 1]]
Matriz B: tamaño (2, 2)
[[ 6 10]
[ 8  2]]
Matriz C: tamaño (2, 2)
[[ 9 25]
[16  1]]
Matriz D: tamaño (2, 2)
[[ 0.28224002 -1.91784855]
[-1.51360499  1.68294197]]

6.2. Funções sobre matrizes

Como pode ser visto no último cálculo, NumPy oferece operadores de funções sobre matrizes, há uma infinidade de funções que podem ser realizadas sobre matrizes, matemáticas, lógicas, de álgebra linear, etc. A seguir mostramos algumas

	
		
			< >
			Input
		
		
			Python
			
		
	
	
		A = np.array([[3, 5], [4, 1]])
 
print(f"A
{A}
")
 
print(f"exp(A)
{np.exp(A)}
")
print(f"sqrt(A)
{np.sqrt(A)}
")
print(f"cos(A)
{np.cos(A)}
")
	
	Copied

>_ Output

			
				A
[[3 5]
[4 1]]
exp(A)
[[ 20.08553692 148.4131591 ]
[ 54.59815003   2.71828183]]
sqrt(A)
[[1.73205081 2.23606798]
[2.         1.        ]]
cos(A)
[[-0.9899925   0.28366219]
[-0.65364362  0.54030231]]

Há algumas funções que retornam informações das matrizes, como a média

	
		
			< >
			Input
		
		
			Python
			
		
	
	
		A = np.array([[3, 5], [4, 1]])
 
print(f"A
{A}
")
 
print(f"A.mean()
{A.mean()}
")
	
	Copied

>_ Output

			
				A
[[3 5]
[4 1]]
A.mean()
3.25

No entanto, podemos obter tais informações de cada eixo por meio do atributo axis. Se for 0, é feito em cada coluna; enquanto se for 1, é feito em cada linha.

	
		
			< >
			Input
		
		
			Python
			
		
	
	
		A = np.array([[3, 5], [4, 1]])
 
print(f"A
{A}
")
 
print(f"A.mean() columnas
{A.mean(axis=0)}
")
print(f"A.mean() filas
{A.mean(axis=1)}
")
	
	Copied

>_ Output

			
				A
[[3 5]
[4 1]]
A.mean() columnas
[3.5 3. ]
A.mean() filas
[4.  2.5]

6.3. Transmissão

Operações matriciais podem ser realizadas com matrizes de diferentes dimensões. Neste caso, o NumPy detectará isso e fará uma projeção da menor matriz até igualá-la à maior.

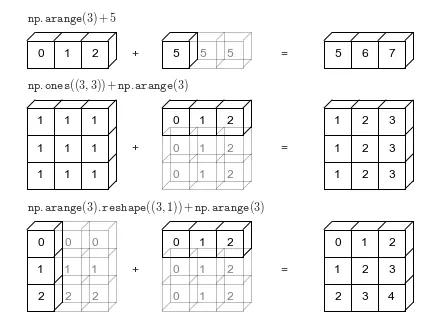
Esta é uma grande qualidade do NumPy, que permite realizar cálculos em matrizes sem ter que se preocupar com a correspondência das dimensões dessas matrizes.

	
		
			< >
			Input
		
		
			Python
			
		
	
	
		A = np.array([1, 2, 3])
 
print(f"A
{A}
")
 
B = A + 5
 
print(f"B
{B}
")
	
	Copied

>_ Output

			
				A
[1 2 3]
B
[6 7 8]

	
		
			< >
			Input
		
		
			Python
			
		
	
	
		A = np.array([1, 2, 3])
B = np.ones((3,3))
 
print(f"A
{A}
")
print(f"B
{B}
")
 
C = A + B
 
print(f"C
{C}
")
	
	Copied

>_ Output

			
				A
[1 2 3]
B
[[1. 1. 1.]
[1. 1. 1.]
[1. 1. 1.]]
C
[[2. 3. 4.]
[2. 3. 4.]
[2. 3. 4.]]

	
		
			< >
			Input
		
		
			Python
			
		
	
	
		A = np.array([1, 2, 3])
B = np.array([[1], [2], [3]])
 
print(f"A
{A}
")
print(f"B
{B}
")
 
C = A + B
 
print(f"C
{C}
")
	
	Copied

>_ Output

			
				A
[1 2 3]
B
[[1]
[2]
[3]]
C
[[2 3 4]
[3 4 5]
[4 5 6]]

7. Indexação de matrizes

O indexação de matrizes é feita da mesma forma que com as listas do Python

	
		
			< >
			Input
		
		
			Python
			
		
	
	
		arr = np.array([1, 2, 3, 4, 5])
arr[3]
	
	Copied

>_ Output

No caso de ter mais de uma dimensão, deve-se indicar o índice em cada uma delas

	
		
			< >
			Input
		
		
			Python
			
		
	
	
		arr = np.array([[1, 2, 3, 4, 5],
                [6, 7, 8, 9, 10]])
arr[1, 2]
	
	Copied

>_ Output

Pode-se usar a indexação negativa

	
		
			< >
			Input
		
		
			Python
			
		
	
	
		arr[-1, -2]
	
	Copied

>_ Output

Em caso de não indicar um dos eixos, considera-se que se quer o completo

	
		
			< >
			Input
		
		
			Python
			
		
	
	
		arr = np.array([[1, 2, 3, 4, 5],
                [6, 7, 8, 9, 10]])
arr[1]
	
	Copied

>_ Output

			
				array([ 6,  7,  8,  9, 10])

7.1. Fatias de matrizes

Na hora de indexar, podemos ficar com partes de matrizes da mesma forma que era feito com as listas do Python.

Lembre-se de que era feito da seguinte maneira:

início:fim:passo

Onde o intervalo vai do start (inclusivo) até o stop (exclusivo) com um passo de step

Se step não for indicado, por padrão é 1

Por exemplo, se quisermos itens da segunda linha e da segunda à quarta coluna:

Selecionamos a segunda linha com um 1 (já que se começa a contar do 0)
Selecionamos da segunda à quarta linha usando 1:4, onde o 1 indica a segunda coluna e o 4 indica a quinta (já que o segundo número indica a coluna em que se termina sem incluir essa coluna). Os dois números levando em conta que a contagem começa a partir de 0

	
		
			< >
			Input
		
		
			Python
			
		
	
	
		print(arr)
print(arr[1, 1:4])
	
	Copied

>_ Output

			
				[[ 1  2  3  4  5]
[ 6  7  8  9 10]]
[7 8 9]

Podemos pegar desde uma posição até o final

	
		
			< >
			Input
		
		
			Python
			
		
	
	
		arr[1, 2:]
	
	Copied

>_ Output

			
				array([ 8,  9, 10])

Desde o início até uma posição

	
		
			< >
			Input
		
		
			Python
			
		
	
	
		arr[1, :3]
	
	Copied

>_ Output

			
				array([6, 7, 8])

Definir o intervalo com números negativos

	
		
			< >
			Input
		
		
			Python
			
		
	
	
		arr[1, -3:-1]
	
	Copied

>_ Output

			
				array([8, 9])

Escolher o passo

	
		
			< >
			Input
		
		
			Python
			
		
	
	
		arr[1, 1:4:2]
	
	Copied

>_ Output

			
				array([7, 9])

7.2. Iteração sobre matrizes

A iteração sobre matrizes multidimensionais é realizada em relação ao primeiro eixo

	
		
			< >
			Input
		
		
			Python
			
		
	
	
		M = np.array( [[[ 0, 1, 2],
                [ 10, 12, 13]],
               [[100,101,102],
                [110,112,113]]])
 
print(f'Matriz de dimensión: {M.shape}
')
 
i = 0
for fila in M:
  print(f'Fila {i}: {fila}')
  i += 1
	
	Copied

>_ Output

			
				Matriz de dimensión: (2, 2, 3)
Fila 0: [[ 0  1  2]
[10 12 13]]
Fila 1: [[100 101 102]
[110 112 113]]

No entanto, se o que queremos é iterar por cada item, podemos usar o método 'flat'

	
		
			< >
			Input
		
		
			Python
			
		
	
	
		i = 0
for fila in M.flat:
  print(f'Elemento {i}: {fila}')
  i += 1
	
	Copied

>_ Output

			
				Elemento 0: 0
Elemento 1: 1
Elemento 2: 2
Elemento 3: 10
Elemento 4: 12
Elemento 5: 13
Elemento 6: 100
Elemento 7: 101
Elemento 8: 102
Elemento 9: 110
Elemento 10: 112
Elemento 11: 113

8. Cópia de matrizes

Em NumPy temos duas maneiras de copiar arrays: através de copy, que realiza uma cópia nova do array, e através de view, que realiza uma visualização do array original.

A cópia é proprietária dos dados e qualquer alteração realizada na cópia não afetará a matriz original, e qualquer alteração realizada na matriz original não afetará a cópia.

A visualização não é proprietária dos dados e qualquer alteração realizada na cópia afetará a matriz original, e qualquer alteração realizada na matriz original afetará a cópia.

8.1. Cópia

	
		
			< >
			Input
		
		
			Python
			
		
	
	
		arr = np.array([1, 2, 3, 4, 5])
copy_arr = arr.copy()
arr[0] = 42
copy_arr[1] = 43
 
print(f'Original: {arr}')
print(f'Copia:    {copy_arr}')
	
	Copied

>_ Output

			
				Original: [42  2  3  4  5]
Copia:    [ 1 43  3  4  5]

8.2. Visão

	
		
			< >
			Input
		
		
			Python
			
		
	
	
		arr = np.array([1, 2, 3, 4, 5])
view_arr = arr.view()
arr[0] = 42
view_arr[1] = 43
 
print(f'Original: {arr}')
print(f'Vista:    {view_arr}')
	
	Copied

>_ Output

			
				Original: [42 43  3  4  5]
Vista:    [42 43  3  4  5]

8.3. Proprietário dos dados

Diante da dúvida se temos uma cópia ou uma visão, podemos usar base

	
		
			< >
			Input
		
		
			Python
			
		
	
	
		arr = np.array([1, 2, 3, 4, 5])
 
copy_arr = arr.copy()
view_arr = arr.view()
 
print(copy_arr.base)
print(view_arr.base)
	
	Copied

>_ Output

			
				None
[1 2 3 4 5]

9. Forma das matrizes

Podemos saber a forma que tem a matriz através do método shape. Este nos retornará uma tupla, o tamanho da tupla representa as dimensões da matriz, em cada elemento da tupla é indicado o número de itens em cada uma das dimensões da matriz.

	
		
			< >
			Input
		
		
			Python
			
		
	
	
		arr = np.array([
                [[1, 2, 3, 4, 5],
                [6, 7, 8, 9, 10]],
                
                [[11, 12, 13, 14, 15],
                [16, 17, 18, 19, 20]]
                ])
 
print(arr)
print(arr.shape)
	
	Copied

>_ Output

			
				[[[ 1  2  3  4  5]
  [ 6  7  8  9 10]]
[[11 12 13 14 15]
  [16 17 18 19 20]]]
(2, 2, 5)

9.1. Reshape

Podemos mudar a forma das matrizes para aquela que desejarmos através do método reshape.

Por exemplo, a matriz anterior, que tem uma forma de (2, 2, 4). Podemos passá-la para (5, 4).

	
		
			< >
			Input
		
		
			Python
			
		
	
	
		arr_reshape = arr.reshape(5, 4)
 
print(arr_reshape)
print(arr_reshape.shape)
	
	Copied

>_ Output

			
				[[ 1  2  3  4]
[ 5  6  7  8]
[ 9 10 11 12]
[13 14 15 16]
[17 18 19 20]]
(5, 4)

Deve-se ter em conta que para redimensionar as matrizes, o número de itens da nova forma deve ser igual ao número de itens da primeira forma.

Isto é, no exemplo anterior, a primeira matriz tinha 20 itens (2x2x4), e a nova matriz tem 20 itens (5x4). O que não podemos fazer é redimensioná-la para uma matriz de tamanho (3, 4), pois no total haveria 12 itens.

	
		
			< >
			Input
		
		
			Python
			
		
	
	
		arr_reshape = arr.reshape(3, 4)
	
	Copied

>_ Output

			
				---------------------------------------------------------------------------ValueError                                Traceback (most recent call last)&lt;ipython-input-12-29e85875d1df&gt; in &lt;module&gt;()
----&gt; 1 arr_reshape = arr.reshape(3, 4)
ValueError: cannot reshape array of size 20 into shape (3,4)

9.2. Dimensão desconhecida

No caso de quisermos mudar a forma de uma matriz e uma das dimensões não importar ou desconhecermos, podemos fazer com que o NumPy a calcule para nós inserindo um -1 como parâmetro.

	
		
			< >
			Input
		
		
			Python
			
		
	
	
		arr = np.array([
                [[1, 2, 3, 4, 5],
                [6, 7, 8, 9, 10]],
                
                [[11, 12, 13, 14, 15],
                [16, 17, 18, 19, 20]]
                ])
 
arr_reshape = arr.reshape(2, -1)
 
print(arr_reshape)
print(arr_reshape.shape)
	
	Copied

>_ Output

			
				[[ 1  2  3  4  5  6  7  8  9 10]
[11 12 13 14 15 16 17 18 19 20]]
(2, 10)

Deve-se ter em conta que não se pode colocar qualquer número nas dimensões conhecidas. O número de itens da matriz original deve ser um múltiplo das dimensões conhecidas.

No exemplo anterior, a matriz tem 20 itens, que é múltiplo de 2, dimensão conhecida introduzida. Não seria possível colocar um 3 como dimensão conhecida, já que 20 não é múltiplo de 3, e não haveria nenhum número que pudesse ser colocado na dimensão desconhecida que fizesse com que, no total, houvesse 20 itens.

9.3. Achatamento de matrizes

Podemos aplanar as matrizes, ou seja, passá-las para uma única dimensão usando reshape(-1). Desta forma, independentemente das dimensões da matriz original, a nova sempre terá uma única dimensão.

	
		
			< >
			Input
		
		
			Python
			
		
	
	
		arr = np.array([
                [[1, 2, 3, 4, 5],
                [6, 7, 8, 9, 10]],
                
                [[11, 12, 13, 14, 15],
                [16, 17, 18, 19, 20]]
                ])
 
arr_flatten = arr.reshape(-1)
 
print(arr_flatten)
print(arr_flatten.shape)
	
	Copied

>_ Output

			
				[ 1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17 18 19 20]
(20,)

Outra forma de aplanar uma matriz é através do método ravel()

	
		
			< >
			Input
		
		
			Python
			
		
	
	
		arr = np.array([
                [[1, 2, 3, 4, 5],
                [6, 7, 8, 9, 10]],
                
                [[11, 12, 13, 14, 15],
                [16, 17, 18, 19, 20]]
                ])
 
arr_flatten = arr.ravel()
 
print(arr_flatten)
print(arr_flatten.shape)
	
	Copied

>_ Output

			
				[ 1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17 18 19 20]
(20,)

9.4. Matriz transposta

Pode-se obter a transposta de uma matriz através do método T. Fazer a transposta de uma matriz é trocar as linhas pelas colunas da matriz, na imagem seguinte vemos um exemplo que esclarece melhor.

	
		
			< >
			Input
		
		
			Python
			
		
	
	
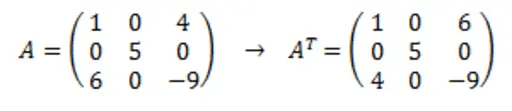
		arr = np.array([[1, 0, 4],
                [0, 5, 0],
                [6, 0, -9]])
 
arr_t = arr.T
 
print(arr_t)
print(arr_t.shape)
	
	Copied

>_ Output

			
				[[ 1  0  6]
[ 0  5  0]
[ 4  0 -9]]
(3, 3)

10. Empilhamento de matrizes

10.1. Empilhamento vertical

Matrizes podem ser empilhadas verticalmente (juntando linhas) usando o método vstack().

	
		
			< >
			Input
		
		
			Python
			
		
	
	
		a = np.array([[1, 1, 1],
              [2, 2, 2],
              [3, 3, 3]])
 
b = np.array([[4, 4, 4],
              [5, 5, 5],
              [6, 6, 6]])
 
c = np.vstack((a,b))
c
	
	Copied

>_ Output

			
				array([[1, 1, 1],
       [2, 2, 2],
       [3, 3, 3],
       [4, 4, 4],
       [5, 5, 5],
       [6, 6, 6]])

Se tiver matrizes com mais de 2 dimensões, vstack() empilhará ao longo da primeira dimensão.

	
		
			< >
			Input
		
		
			Python
			
		
	
	
		a = np.array([
                [[1, 1],
                [2, 2]],
                
                [[3, 3],
                [4, 4]]
                ])
 
b = np.array([
                [[5, 5],
                [6, 6]],
                
                [[7, 7],
                [8, 8]]
                ])
 
c = np.vstack((a,b))
c
	
	Copied

>_ Output

			
				array([[[1, 1],
        [2, 2]],
       [[3, 3],
        [4, 4]],
       [[5, 5],
        [6, 6]],
       [[7, 7],
        [8, 8]]])

10.2. Empilhamento horizontal

Matrizes podem ser empilhadas horizontalmente (juntando colunas) através do método hstack()

	
		
			< >
			Input
		
		
			Python
			
		
	
	
		a = np.array([[1, 2, 3],
              [1, 2, 3],
              [1, 2, 3]])
 
b = np.array([[4, 5, 6],
              [4, 5, 6],
              [4, 5, 6]])
 
c = np.hstack((a,b))
c
	
	Copied

>_ Output

			
				array([[1, 2, 3, 4, 5, 6],
       [1, 2, 3, 4, 5, 6],
       [1, 2, 3, 4, 5, 6]])

Se tiver matrizes com mais de 2 dimensões, hstack() empilhará ao longo da segunda dimensão.

	
		
			< >
			Input
		
		
			Python
			
		
	
	
		a = np.array([
                [[1, 1],
                [2, 2]],
                
                [[3, 3],
                [4, 4]]
                ])
 
b = np.array([
                [[5, 5],
                [6, 6]],
                
                [[7, 7],
                [8, 8]]
                ])
 
c = np.hstack((a,b))
c
	
	Copied

>_ Output

			
				array([[[1, 1],
        [2, 2],
        [5, 5],
        [6, 6]],
       [[3, 3],
        [4, 4],
        [7, 7],
        [8, 8]]])

Outra maneira de adicionar colunas a uma matriz é através do método column_stack()

	
		
			< >
			Input
		
		
			Python
			
		
	
	
		a = np.array([[1, 2, 3],
              [1, 2, 3],
              [1, 2, 3]])
 
b = np.array([4, 4, 4])
 
c = np.column_stack((a,b))
c
	
	Copied

>_ Output

			
				array([[1, 2, 3, 4],
       [1, 2, 3, 4],
       [1, 2, 3, 4]])

10.3. Empilhamento em profundidade

Matrizes podem ser empilhadas em profundidade (terceira dimensão) usando o método dstack()

	
		
			< >
			Input
		
		
			Python
			
		
	
	
		a = np.array([
                [[1, 1],
                [2, 2]],
                
                [[3, 3],
                [4, 4]]
                ])
 
b = np.array([
                [[1, 1],
                [2, 2]],
                
                [[3, 3],
                [4, 4]]
                ])
 
c = np.dstack((a,b))
print(f"c: {c}
")
print(f"a.shape: {a.shape}, b.shape: {b.shape}, c.shape: {c.shape}")
	
	Copied

>_ Output

			
				c: [[[1 1 1 1]
  [2 2 2 2]]
[[3 3 3 3]
  [4 4 4 4]]]
a.shape: (2, 2, 2), b.shape: (2, 2, 2), c.shape: (2, 2, 4)

Se tiver matrizes com mais de 4 dimensões, dstack() empilhará ao longo da terceira dimensão.

	
		
			< >
			Input
		
		
			Python
			
		
	
	
		a = np.array([1, 2, 3, 4, 5], ndmin=4)
 
b = np.array([1, 2, 3, 4, 5], ndmin=4)
 
c = np.dstack((a,b))
print(f"a.shape: {a.shape}, b.shape: {b.shape}, c.shape: {c.shape}")
	
	Copied

>_ Output

			
				a.shape: (1, 1, 1, 5), b.shape: (1, 1, 1, 5), c.shape: (1, 1, 2, 5)

10.3. Empilhamento personalizado

Por meio do método concatenate(), é possível escolher o eixo ao longo do qual as matrizes serão empilhadas.

	
		
			< >
			Input
		
		
			Python
			
		
	
	
		a = np.array([
                [[1, 1],
                [2, 2]],
                
                [[3, 3],
                [4, 4]]
                ])
 
b = np.array([
                [[5, 5],
                [6, 6]],
                
                [[7, 7],
                [8, 8]]
                ])
 
conc0 = np.concatenate((a,b), axis=0) # concatenamiento en el primer eje
conc1 = np.concatenate((a,b), axis=1) # concatenamiento en el segundo eje
conc2 = np.concatenate((a,b), axis=2) # concatenamiento en el tercer eje
print(f"conc0: {conc0}
")
print(f"conc1: {conc1}
")
print(f"conc2: {conc2}")
	
	Copied

>_ Output

			
				conc0: [[[1 1]
  [2 2]]
[[3 3]
  [4 4]]
[[5 5]
  [6 6]]
[[7 7]
  [8 8]]]
conc1: [[[1 1]
  [2 2]
  [5 5]
  [6 6]]
[[3 3]
  [4 4]
  [7 7]
  [8 8]]]
conc2: [[[1 1 5 5]
  [2 2 6 6]]
[[3 3 7 7]
  [4 4 8 8]]]

11. Dividir matrizes

11.1. Dividir verticalmente

Matrizes podem ser divididas verticalmente (separando linhas) através do método vsplit()

	
		
			< >
			Input
		
		
			Python
			
		
	
	
		a = np.array([[1.1, 1.2, 1.3, 1.4],
              [2.1, 2.2, 2.3, 2.4],
              [3.1, 3.2, 3.3, 3.4],
              [4.1, 4.2, 4.3, 4.4]])
 
[a1, a2] = np.vsplit(a, 2)
print(f"a1: {a1}
")
print(f"a2: {a2}")
	
	Copied

>_ Output

			
				a1: [[1.1 1.2 1.3 1.4]
[2.1 2.2 2.3 2.4]]
a2: [[3.1 3.2 3.3 3.4]
[4.1 4.2 4.3 4.4]]

Se tiver matrizes com mais de 2 dimensões, vsplit() dividirá ao longo da primeira dimensão.

	
		
			< >
			Input
		
		
			Python
			
		
	
	
		a = np.array([
                [[1, 1],
                [2, 2]],
                
                [[3, 3],
                [4, 4]]
                ])
 
[a1, a2] = np.vsplit(a, 2)
print(f"a1: {a1}
")
print(f"a2: {a2}")
	
	Copied

>_ Output

			
				a1: [[[1 1]
  [2 2]]]
a2: [[[3 3]
  [4 4]]]

11.2. Dividir horizontalmente

Matrizes podem ser divididas horizontalmente (separando colunas) através do método hsplit()

	
		
			< >
			Input
		
		
			Python
			
		
	
	
		a = np.array([[1.1, 1.2, 1.3, 1.4],
              [2.1, 2.2, 2.3, 2.4],
              [3.1, 3.2, 3.3, 3.4],
              [4.1, 4.2, 4.3, 4.4]])
 
[a1, a2] = np.hsplit(a, 2)
print(f"a1: {a1}
")
print(f"a2: {a2}")
	
	Copied

>_ Output

			
				a1: [[1.1 1.2]
[2.1 2.2]
[3.1 3.2]
[4.1 4.2]]
a2: [[1.3 1.4]
[2.3 2.4]
[3.3 3.4]
[4.3 4.4]]

Se tiver matrizes com mais de 2 dimensões, hsplit() dividirá ao longo da segunda dimensão.

	
		
			< >
			Input
		
		
			Python
			
		
	
	
		a = np.array([
                [[1, 1],
                [2, 2]],
                
                [[3, 3],
                [4, 4]]
                ])
 
[a1, a2] = np.hsplit(a, 2)
print(f"a1: {a1}
")
print(f"a2: {a2}")
	
	Copied

>_ Output

			
				a1: [[[1 1]]
[[3 3]]]
a2: [[[2 2]]
[[4 4]]]

11.3. Dividir de maneira personalizada

Com o método array_split(), é possível escolher o eixo em que se deseja dividir as matrizes.

	
		
			< >
			Input
		
		
			Python
			
		
	
	
		a = np.array([
                [[1, 1],
                [2, 2]],
                
                [[3, 3],
                [4, 4]]
                ])
 
[a1_eje0, a2_eje0] = np.array_split(a, 2, axis=0)
[a1_eje1, a2_eje1] = np.array_split(a, 2, axis=1)
[a1_eje2, a2_eje2] = np.array_split(a, 2, axis=2)
 
print(f"a1_eje0: {a1_eje0}
")
print(f"a2_eje0: {a2_eje0}

")
 
print(f"a1_eje1: {a1_eje1}
")
print(f"a2_eje1: {a2_eje1}

")
 
print(f"a1_eje2: {a1_eje2}
")
print(f"a2_eje2: {a2_eje2}")
	
	Copied

>_ Output

			
				a1_eje0: [[[1 1]
  [2 2]]]
a2_eje0: [[[3 3]
  [4 4]]]
a1_eje1: [[[1 1]]
[[3 3]]]
a2_eje1: [[[2 2]]
[[4 4]]]
a1_eje2: [[[1]
  [2]]
[[3]
  [4]]]
a2_eje2: [[[1]
  [2]]
[[3]
  [4]]]

12. Busca em matrizes

Se quiser buscar um valor dentro de uma matriz, pode-se usar o método where() que retorna as posições onde a matriz possui o valor que estamos procurando.

	
		
			< >
			Input
		
		
			Python
			
		
	
	
		arr = np.array([1, 2, 3, 4, 5, 4, 4])
 
ids = np.where(arr == 4)
ids
	
	Copied

>_ Output

			
				(array([3, 5, 6]),)

Funções podem ser usadas para buscar, por exemplo, se quisermos encontrar em quais posições os valores são pares

	
		
			< >
			Input
		
		
			Python
			
		
	
	
		arr = np.array([1, 2, 3, 4, 5, 6, 7, 8])
 
ids = np.where(arr%2)
ids
	
	Copied

>_ Output

			
				(array([0, 2, 4, 6]),)

13. Ordenar matrizes

Com o método sort() podemos ordenar arrays

	
		
			< >
			Input
		
		
			Python
			
		
	
	
		arr = np.array([3, 2, 0, 1])
 
arr_ordenado = np.sort(arr)
arr_ordenado
	
	Copied

>_ Output

			
				array([0, 1, 2, 3])

Se temos strings, eles são ordenados alfabeticamente

	
		
			< >
			Input
		
		
			Python
			
		
	
	
		arr = np.array(['banana', 'apple', 'cherry'])
 
arr_ordenado = np.sort(arr)
arr_ordenado
	
	Copied

>_ Output

			
				array(['apple', 'banana', 'cherry'], dtype='&lt;U6')

E as matrizes de booleanos também são ordenadas

	
		
			< >
			Input
		
		
			Python
			
		
	
	
		arr = np.array([True, False, True])
 
arr_ordenado = np.sort(arr)
arr_ordenado
	
	Copied

>_ Output

			
				array([False,  True,  True])

Se tiver matrizes de mais de uma dimensão, as ordena por dimensões, ou seja, se tiver uma matriz de 2 dimensões, ordena os números da primeira linha entre si e os da segunda linha entre si.

	
		
			< >
			Input
		
		
			Python
			
		
	
	
		arr = np.array([[3, 2, 4], [5, 0, 1]])
 
arr_ordenado = np.sort(arr)
arr_ordenado
	
	Copied

>_ Output

			
				array([[2, 3, 4],
       [0, 1, 5]])

Por padrão, ordena sempre com relação às linhas, mas se quiser que ordene com relação a outra dimensão, deve ser especificado através da variável axis.

	
		
			< >
			Input
		
		
			Python
			
		
	
	
		arr = np.array([[3, 2, 4], [5, 0, 1]])
 
arr_ordenado0 = np.sort(arr, axis=0) # Se ordena con respecto a la primera dimensión
arr_ordenado1 = np.sort(arr, axis=1) # Se ordena con respecto a la segunda dimensión
 
print(f"arr_ordenado0: {arr_ordenado0}
")
print(f"arr_ordenado1: {arr_ordenado1}
")
	
	Copied

>_ Output

			
				arr_ordenado0: [[3 0 1]
[5 2 4]]
arr_ordenado1: [[2 3 4]
[0 1 5]]

14. Filtros em matrizes

NumPy oferece a possibilidade de buscar certos elementos de uma matriz e criar uma nova

Isso é feito criando uma matriz de índices booleanos, ou seja, cria uma nova matriz que indica quais posições mantemos da matriz e quais não.

Vamos ver um exemplo de uma matriz de índices booleanos

	
		
			< >
			Input
		
		
			Python
			
		
	
	
		arr = np.array([37, 85, 12, 45, 69, 22])
 
indices_booleanos = [False, False, True, False, False, True]
 
arr_filter = arr[indices_booleanos]
 
print(f"Array original: {arr}")
print(f"indices booleanos: {indices_booleanos}")
print(f"Array filtrado: {arr_filter}")
	
	Copied

>_ Output

			
				Array original: [37 85 12 45 69 22]
indices booleanos: [False, False, True, False, False, True]
Array filtrado: [12 22]

Como se pode ver, o array filtrado (arr_filtr), só ficou com os elementos do array original (arr) que correspondem aos elementos em que o array indices_booleanos é True

Outra coisa que podemos observar é que apenas os elementos pares foram mantidos, então agora vamos ver como fazer para manter apenas os elementos pares de uma matriz, sem ter que fazê-lo manualmente como fizemos no exemplo anterior.

	
		
			< >
			Input
		
		
			Python
			
		
	
	
		arr = np.array([[1, 2, 3, 4, 5],
                [6, 7, 8, 9, 10]])
 
indices_booleanos = arr % 2 == 0
 
arr_filter = arr[indices_booleanos]
 
print(f"Array original: {arr}
")
print(f"indices booleanos: {indices_booleanos}
")
print(f"Array filtrado: {arr_filter}")
	
	Copied

>_ Output

			
				Array original: [[ 1  2  3  4  5]
[ 6  7  8  9 10]]
indices booleanos: [[False  True False  True False]
[ True False  True False  True]]
Array filtrado: [ 2  4  6  8 10]

Continuar lendo

Deep Research com LangGraph: Crie um Assistente de IA para Pesquisar Automaticamente

Aprenda como funcionam as redes neurais do zero com um exemplo prático de regressão linear. Tutorial passo a passo que explica neurônios artificiais, inicialização de parâmetros, funções de perda e erro quadrático médio (EQM) com código Python.

Elicitação MCP: Implementar Elicitação em Servidores com FastMCP e Python

Aprenda a implementar elicitação em servidores MCP (Model Context Protocol) com FastMCP. Tutorial completo passo a passo...

MCP Durabilidade: Servidor e Cliente com Persistência para Tarefas de Longa Duração

Aprenda a construir servidor e cliente MCP com durabilidade para tarefas de longa duração. Tutorial completo do Model Co...

Últimos posts -->

Você viu esses projetos?

Gymnasia

Horeca chatbot

Naviground

Ver todos os projetos -->

>_ Disponível para projetos

Tem um projeto com IA?

Vamos conversar.

maximofn@gmail.com

Especialista em Machine Learning e Inteligência Artificial. Desenvolvo soluções com IA generativa, agentes inteligentes e modelos personalizados.

Escreva-me LinkedIn

Quer assistir alguma palestra?

Agentes do Amanhã: Descifrando os Mistérios da Planificação, UX e Memória

Agentes de IA, impulsionados por LLMs, prometem transformar aplicações. Mas eles são meros executores hoje ou futuros colaboradores inteligentes? Para...

Crie sua própria inteligência Apple

Aprenda a criar um sistema de IA para executar eficientemente em um dispositivo

Últimas palestras -->

Quer melhorar com essas dicas?

o1 prompt engineering

Criar prompts melhores para o1 seguindo um exemplo

Memory profiler

Ver o uso de memória de um script

DataLoader com pin_memory e num_workers

Aumentar o desempenho de DataLoader com pin_memory e num_workers

Últimos tips -->

Use isso localmente

Os espaços do Hugging Face nos permitem executar modelos com demos muito simples, mas e se a demo quebrar? Ou se o usuário a deletar? Por isso, criei contêineres docker com alguns espaços interessantes, para poder usá-los localmente, aconteça o que acontecer. Na verdade, se você clicar em qualquer botão de visualização de projeto, ele pode levá-lo a um espaço que não funciona.

Flow edit

FLUX.1-RealismLora

token_hmr

Ver todos os contêineres -->

>_ Disponível para projetos

Tem um projeto com IA?

Vamos conversar.

maximofn@gmail.com

Especialista em Machine Learning e Inteligência Artificial. Desenvolvo soluções com IA generativa, agentes inteligentes e modelos personalizados.

Escreva-me LinkedIn

Você quer treinar seu modelo com esses datasets?

short-jokes-dataset

HuggingFace

Dataset com piadas em inglês

Uso: Fine-tuning de modelos de geração de texto humorístico

231K linhas 2 colunas 45 MB

Ver no HuggingFace →

opus100

HuggingFace

Dataset com traduções de inglês para espanhol

Uso: Treinamento de modelos de tradução inglês-espanhol

1M linhas 2 colunas 210 MB

Ver no HuggingFace →

netflix_titles

HuggingFace

Dataset com filmes e séries da Netflix

Uso: Análise de catálogo Netflix e sistemas de recomendação

8.8K linhas 12 colunas 3.5 MB

Ver no HuggingFace →

Ver mais datasets -->

1. Resumo

2. O que é o NumPy?

2.1. NumPy como np

3. Velocidade do NumPy

4. Matrizes em NumPy

4.1. Como criar matrizes

4.2. Dimensões das matrizes

4.3. Tamanho das matrizes

5. Tipo de dados

6. Operações matemáticas

6.1. Operações básicas

6.2. Funções sobre matrizes

6.3. Transmissão

7. Indexação de matrizes

7.1. Fatias de matrizes

7.2. Iteração sobre matrizes

8. Cópia de matrizes

8.1. Cópia

8.2. Visão

8.3. Proprietário dos dados

9. Forma das matrizes

9.1. Reshape

9.2. Dimensão desconhecida

9.3. Achatamento de matrizes

9.4. Matriz transposta

10. Empilhamento de matrizes

10.1. Empilhamento vertical

10.2. Empilhamento horizontal

10.3. Empilhamento em profundidade

10.3. Empilhamento personalizado

11. Dividir matrizes

11.1. Dividir verticalmente

11.2. Dividir horizontalmente

11.3. Dividir de maneira personalizada

12. Busca em matrizes

13. Ordenar matrizes

14. Filtros em matrizes

Continuar lendo

Deep Research com LangGraph: Crie um Assistente de IA para Pesquisar Automaticamente

Elicitação MCP: Implementar Elicitação em Servidores com FastMCP e Python

MCP Durabilidade: Servidor e Cliente com Persistência para Tarefas de Longa Duração

Você viu esses projetos?

Tem um projeto com IA?

Quer assistir alguma palestra?

Agentes do Amanhã: Descifrando os Mistérios da Planificação, UX e Memória

Crie sua própria inteligência Apple

Quer melhorar com essas dicas?

o1 prompt engineering

Memory profiler

DataLoader com pin_memory e num_workers

Use isso localmente

Tem um projeto com IA?

Você quer treinar seu modelo com esses datasets?

short-jokes-dataset

opus100

netflix_titles

2.1. NumPy como `np`