Los modelos de lenguaje son cada vez más grandes, lo que hace que cada vez sean más costosos y caros de ejecutar.
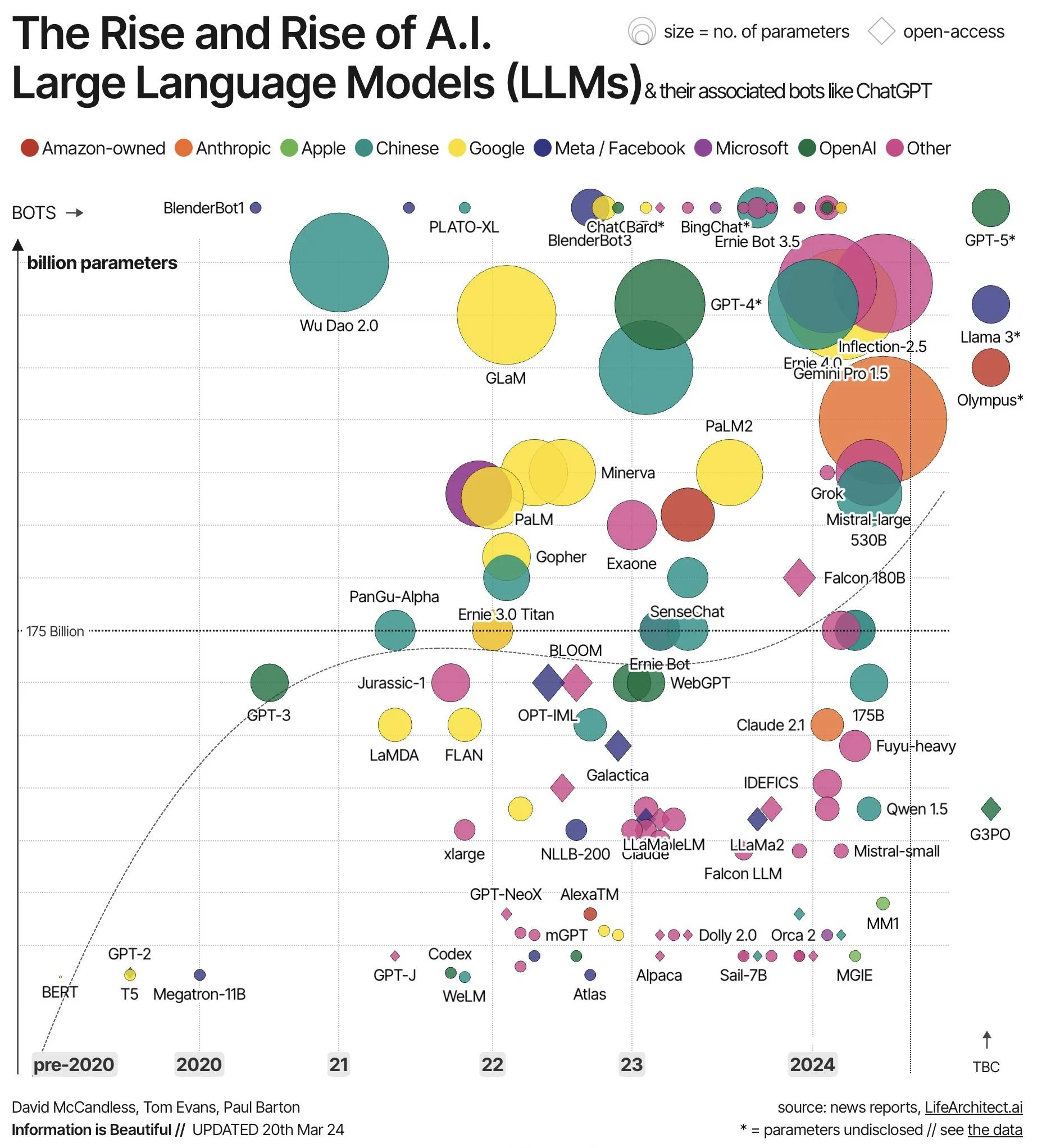

Por ejemplo, el modelo llama 3 400B, si sus parámetros están almacenados en formato FP32, cada parámetro ocupa por tanto 4 bytes, lo que supone que solo para almacenar el modelo hace falta 400*(10e9)*4 bytes = 1.6 TB de memoria VRAM. Esto supone 20 GPUs de 80GB de memoria VRAM cada una, las cuales además no son baratas.
Pero si dejamos a un lado modelos gigantes y nos vamos a modelos con tamaños más comunes, por ejemplo, 70B de parámetros, solo almacenar el modelo supone 70*(10e9)*4 bytes = 280 GB de memoria VRAM, lo que supone 4 GPUs de 80GB de memoria VRAM cada una.
Esto es porque almacenamos los pesos en formato FP32, es decir, que cada parámetro ocupa 4 bytes. Pero qué pasa si conseguimos que cada parámetro ocupe menos bytes? A esto se le llama cuantización.
Por ejemplo, si conseguimos que un modelo de 70B de parámetros, sus parámetros ocupen medio byte, entonces solo necesitaríamos 70*(10e9)*0.5 bytes = 35 GB de memoria VRAM, lo que supone 2 GPUs de 24GB de memoria VRAM cada una, las cuales ya se pueden considerar GPUs de usuarios normales.
Necesitamos por tanto maneras de poder reducir el tamaño de estos modelos. Existen tres formas de hacer eso, la destilación, la poda y la cuantización.
La destilación consiste en entrenar un modelo más pequeño a partir de las salidas del grande. Es decir, una entrada se le mete al modelo pequeño y al grande, se considera que la salida correcta es la del modelo grande, por lo que se realiza el entrenamiento del modelo pequeño de acuerdo con la salida del modelo grande. Pero esto requiere tener almacenado el modelo grande, que no es lo que queremos o podemos hacer.
La poda consiste en eliminar parámetros del modelo haciéndolo cada vez más pequeño. Este método se basa en la idea de que los modelos de lenguaje actuales están sobredimensionados y solo unos pocos parámetros son los que realmente aportan información. Por ello, si conseguimos eliminar los parámetros que no aportan información, conseguiremos un modelo más pequeño. Pero esto no es sencillo a día de hoy, porque no tenemos manera de saber bien qué parámetros son los importantes y cuales no.
Por otro lado, la cuantización consiste en reducir el tamaño de cada uno de los parámetros del modelo. Y es lo que vamos a explicar en este post.
Formato de los parámetros
Los parámetros de los pesos se pueden almacenar en varios tipos de formatos

Originalmente se usaba FP32 para almacenar los parámetros, pero debido a que empezamos a quedarnos sin memoria para almacenar los modelos, se empezaron a pasar a FP16, lo cual no daba malos resultados.
Sin embargo el problema de FP16 es que no alcanza valores tan altos como FP32, por lo que puede darse el caso de desbordamiento de valores, es decir, al realizarse cálculos internos en la red, el resultado sea tan alto que no se pueda representar en FP16, lo que produce errores. Esto ocurre porque el modelo fue entrenado en FP32, lo que hace que todos los posibles cálculos internos sean posibles, pero al pasarse después a FP16 para poder hacer inferencias, algunos cálculos internos pueden producir desbordamientos.
Debido a estos errores de desbordamiento se crearon TF32 y BF16, los cuales tienen la misma cantidad de bits de exponente, lo que hace que puedan llegar a valores tan altos como FP32, pero con la ventaja de ocupar menos memoria por tener menos bits. Sin embargo, ambos al tener menos bits de mantisa, no pueden representar números con tanta precisión como FP32, lo cual puede dar errores de redondeo, pero al menos no obtendremos un error al ejecutar la red. TF32 tiene en total 19 bits, mientras que BF16 tiene 16 bits. Se suele usar más BF16 porque se ahorra más memoria.
Históricamente han existido los formatos INT8 y UINT8, que pueden representar números desde -128 a 127 y de 0 a 255 respectivamente. Aunque son formatos buenos porque permiten ahorrar menos memoria, ya que cada parámetro ocupa 1 byte en comparación de los 4 bytes de FP32, el problema que tienen es que solo pueden representar un rango pequeño de números y además solo enteros, por lo que pueden darse los dos problemas vistos antes, desbordamiento y falta de precisión.
Para solucionar el problema de que los formatos INT8 y UINT8 solo representan números enteros se han creado los formatos FP8 y FP4, pero aún no están muy consolidados, ni tienen un formato muy estandarizado.
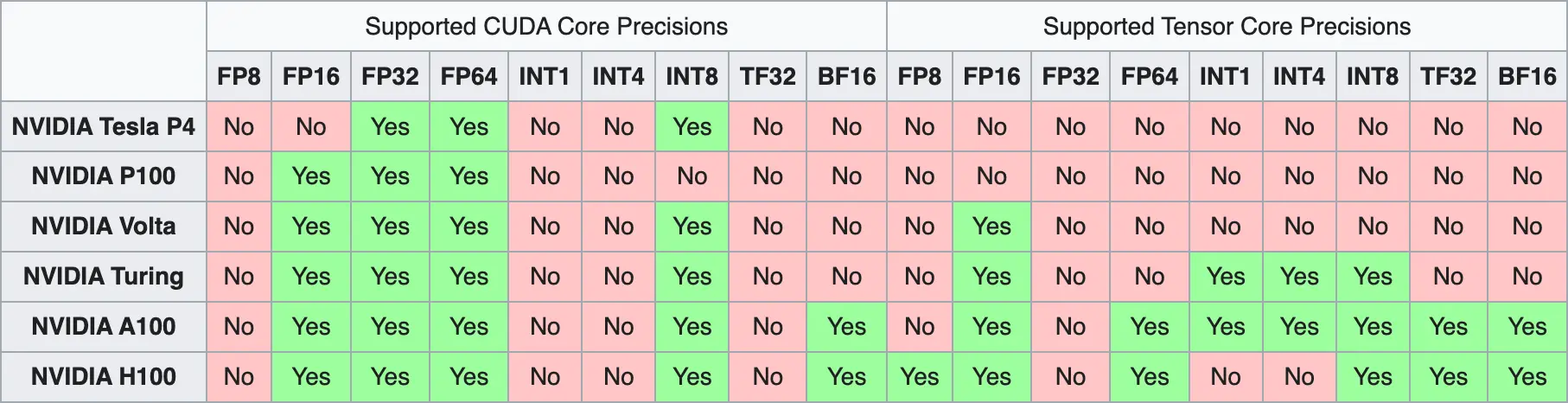
Aunque tengamos manera de poder almacenar los parámetros de los modelos en formatos más pequeños, y aunque consigamos resolver los problemas de desbordamiento y redondeo, tenemos otro problema, y es que no todas las GPUs son capaces de representar todos los formatos. Esto es porque estos problemas de memoria son relativamente nuevos, por lo que las GPUs más antiguas no se diseñaron para poder resolver estos problemas y por tanto no son capaces de representar todos los formatos.
Como último detalle, como curiosidad, durante el entrenamiento de los modelos se utiliza lo que se llama precisión mixta. Los pesos del modelo se almacenan en formato FP32, sin embargo el forward pass y el backward pass se realizan en FP16 para que sea más rápido. Los gradientes resultantes del backward pass se almacenan en FP16 y se usan para modificar los valores FP32 de los pesos.
Tipos de cuantización
Cuantización de punto cero
Este es el tipo de cuantización más sencilla. Consiste en reducir el rango de valores de manera lineal, el mínimo valor de FP32 corresponde al mínimo valor del nuevo formato, el cero de FP32 corresponde al cero del nuevo formato y el máximo valor de FP32 corresponde al máximo valor del nuevo formato.
Por ejemplo, si queremos pasar los números representados desde -1 hasta 1 en formato UINT8, como los límites de UINT8 son -127 y 127, si queremos representar el valor 0.3 lo que hacemos es multiplicar 0.3 por 127, que da 38.1 y redondearlo a 38, que es el valor que se almacenaría en UINT8.
Si queremos hacer el paso contrario, para pasar 38 a formato de entre -1 y 1, lo que hacemos es dividir 38 entre 127, que da 0.2992, que es aproximadamente 0.3, y podemos ver que tenemos un error de 0.008
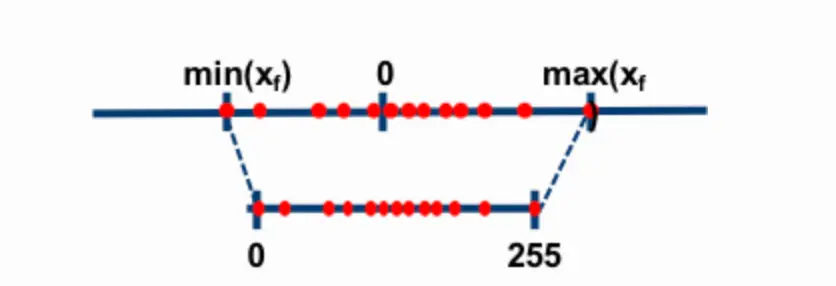
Cuantizazión afin
En este tipo de cuantización, si se tiene un array de valores en un formato y se quiere pasar a otro, primero se divide el array entero por el máximo valor del array y luego se multiplica el array entero por el máximo valor del nuevo formato.
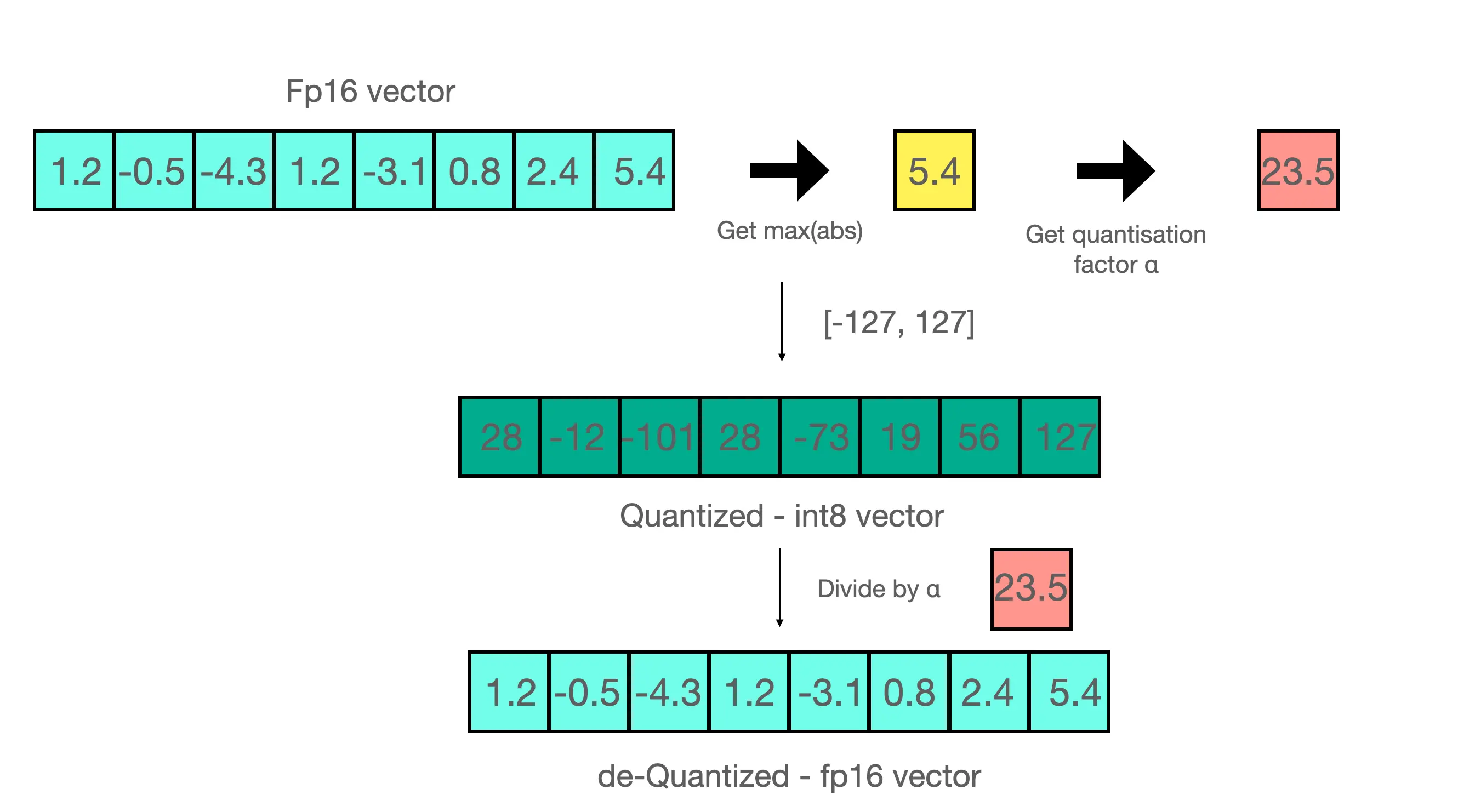
Por ejemplo, en la imagen anterior tenemos el array
[1.2, -0.5, -4.3, 1.2, -3.1, 0.8, 2.4, 5.4]Como su valor máximo es 5.4, dividimos el array por ese valor y obtenemos
[0.2222222222, -0.09259259259, -0.7962962963, 0.2222222222, -0.5740740741, 0.1481481481, 0.4444444444, 1]Si ahora multiplicamos todos los valores por 127, que es el máximo valor de UINT8, obtenemos
[28,22222222, -11.75925926, -101.1296296, 28.22222222, -72.90740741, 18.81481481, 56.44444444, 127]Que, redondeando, sería
[28, -12, -101, 28, -73, 19, 56, 127]Si ahora quisiésemos realizar el paso inverso tendríamos que dividir el array resultante por 127, que daría
[0,2204724409, -0.09448818898, -0.7952755906, 0.2204724409, -0.5748031496, 0.1496062992, 0.4409448819, 1]Y volver a multiplicar por 5.4, con lo que obtendríamos
[1,190551181, -0.5102362205, -4.294488189, 1.190551181, -3.103937008, 0.8078740157, 2.381102362, 5.4]Si lo comparamos con el array original, vemos que tenemos un error
Momentos de cuantización
Cuantización post entrenamiento
Como su nombre indica, la cuantización se produce después del entrenamiento. Se entrena el modelo en FP32 y después se cuantiza a otro formato. Este método es el más sencillo, pero puede dar lugar a errores de precisión en la cuantización
Cuantización durante el entrenamiento
Durante el entrenamiento se realiza el forward pass en el modelo original y en un modelo cuantizado y se ven los posibles errores derivados de la cuantización para poder mitigarlos. Este proceso hace que el entrenamiento sea más costoso, porque tienes que tener almacenado en memoria el modelo original y el cuantizado, y más lento, porque tienes que realizar el forward pass en dos modelos.
Métodos de cuantización
A continuación muestro los enlaces a los posts donde explico cada uno de los métodos para que este post no se haga muy largo
- LLM.int8()
- GPTQ
- QLoRA
- AWQ
- QuIP
- GGUF
- HQQ
- AQLM
- FBGEMM FP8